背景
在 草稿纸上推图形学坐标变换 里推了坐标变换的全过程,为了验证和牢固掌握这些变换,这里将会实现一个基础的只使用CPU进行运算的渲染器。
主要功能
- 显示obj文件
- 点、直线、三角形绘制
- 贴图绘制
具体实现
[1] Bresenham 直线绘制算法
本文介绍著名的Bresenham 直线绘制算法
由于现在的屏幕是由一个个像素点构成的,所以在计算机中绘制的直线也就是只能是由离散的点构成,Bresenham直线绘制算法可以在屏幕上绘制任何直线。并且它只需要使用整除运算,完全不需要浮点运算,从而具有超高的性能。
接下来介绍我理解的Bresenham算法流程,并在最后贴出我实现的C++代码。(为了介绍的容易理解,这里只举斜率为0到1之间的直线)
如下图所示,离散化直线的本质是已知(xi,yi)点时确定下一个点(xi+1,yi+1)的位置:只有两种可能,一种是(xi+1,yi),另一种是(xi+1,yi+1)
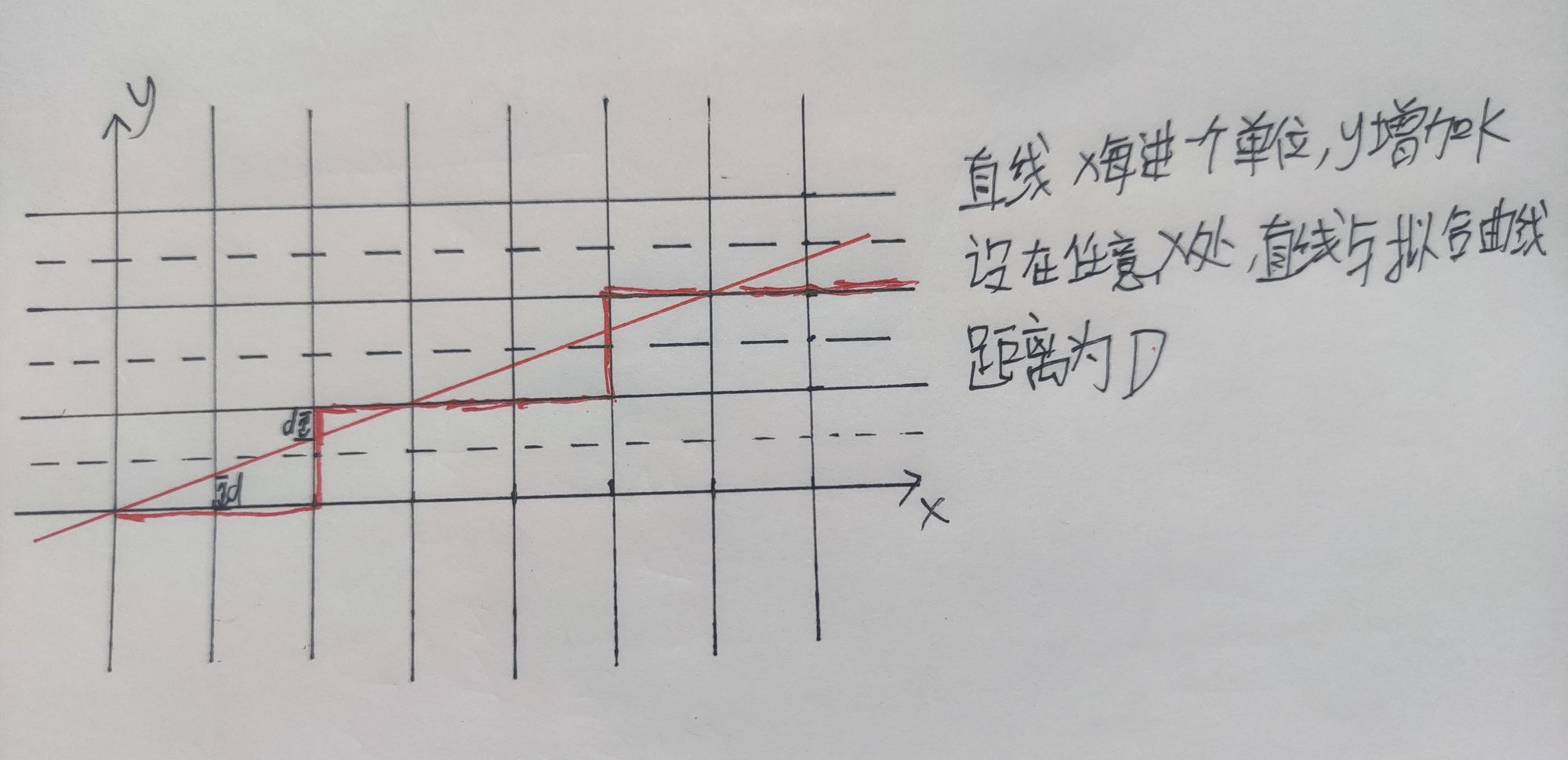
Bresenham算法的核心就是x相同时观察直线到拟合直线的距离(图中的D),距离D超过中点也就是0.5时,拟合曲线就把自己的y值加一,也就是图中移上去一格,从而始终保持D小于等于0.5。
伪代码就是
D=0
for each x in (x0,x1)
DrawPoint(x,y)
D+=k
if(D>0.5)
y++
D-=1 //y移上去之后距离也要更新
这个版本已经可以画任意直线了但是需要浮点运算(比如计算k值,D值)。我们想要更好的性能,于是就有了下面一个优化版本:
首先,我们不想将D与0.5比较(浮点数比较),可以先将D变大一倍不影响结果,此时伪代码变成:
D1=0 //用D1表示新的拟合直线与原直线距离
for each x in (x0,x1)
DrawPoint(x,y)
D1+=2*k
if(D1>1)
y++
D1-=2
由于k=dy/dx,dy=y1-y0,dx=x1-x0,且dy,dx都是整数(输入在屏幕上的点坐标x0,y0,x1,y1一定是整数),于是我们将D扩大dx倍,去掉计算D时候的浮点加法运算,此时伪代码变成:
D2=0 //用D2表示新的拟合直线与原直线距离
for each x in (x0,x1)
DrawPoint(x,y)
D2+=2*dy//整数运算!
if(D2>dx)
y++
D2-=2*dx
于是,我们就得到了一个全部都是整数运算的直线绘制算法!于是它就可以在我之前做的没有浮点运算器的计算机中绘制直线!用Nexys4 DDR 制作一台计算机系列
以下是完整C++代码:
void DrawLine_Bresenham(int x0, int y0, int x1, int y1, const Color& color)
{
if (x1 < x0) {
int tempX, tempY;
tempX = x0;
x0 = x1;
x1 = tempX;
tempY = y0;
y0 = y1;
y1 = tempY;
}
if (x1 == x0) {
for (int y = min(y0, y1); y <= max(y0, y1); y++) {
DrawPoint(x0, y, color);
}
return;
}
//k=0
if (y1==y0) {
for (int x = x0; x < x1; x++) {
DrawPoint(x, y0, color);
}
return;
}
int dx = x1 - x0, dy = y1 - y0;
bool kSign = ((y1 - y0) >= 0 && (x1 - x0) >= 0) ? true : false; //true => positive false =>negative
bool kGreaterThenOne = (abs(y1 - y0) > abs(x1 - x0)) ? true : false;
int d = 0;
// 0<k<=1
if (kSign == true && kGreaterThenOne == false) {
int y = y0;
for (int x = x0; x < x1; x++) {
DrawPoint(x, y, color);
d += 2 * dy;
if (d > dx) {
d -= 2 * dx;
y++;
}
}
}
//k>1
else if (kSign == true && kGreaterThenOne == true) {
int x = x0;
for (int y = y0; y < y1; y++) {
DrawPoint(x, y, color);
d += 2 * dx;
if (d > dy) {
d -= 2 * dy;
x++;
}
}
}
//-1<k<=0
else if(kSign==false&&kGreaterThenOne==false){
int y = y0;
for (int x = x0; x < x1; x++) {
DrawPoint(x, y, color);
d += -2 * dy;
if (d > dx) {
d -= 2 * dx;
y--;
}
}
}
//k<-1
else if (kSign == false && kGreaterThenOne == true) {
int x = x0;
for (int y = y0; y > y1; y--) {
DrawPoint(x, y, color);
d += 2 * dx;
if (d > -dy) {
d -= -2 * dy;
x++;
}
}
}
}
附上用Bresenham直线绘制算法画的兔子
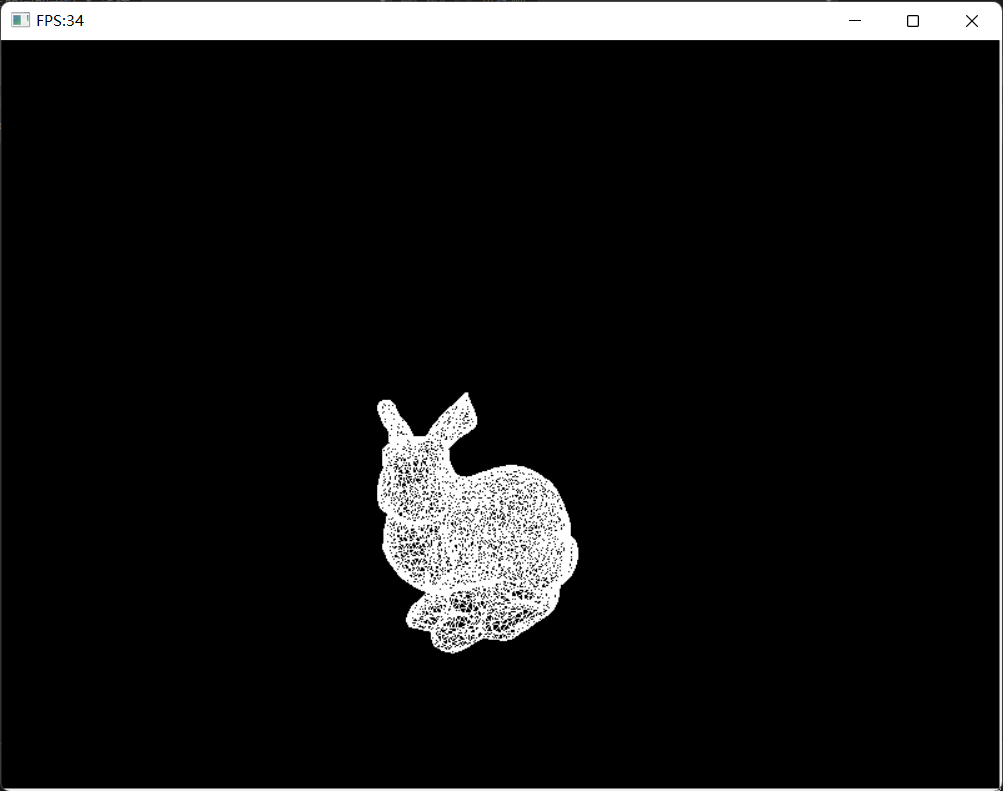
[2]三角形光栅化算法
本文介绍三角形光栅化,大多数软光栅都是以绘制三角面片为基础。
这里介绍经典的拆分法:
如下图所示,所有三角形可以被分类成这三种:
1.朝下的两个点y值相同
2.朝上的两个点y值相同
3.其它的任意三角形(但是拆分成1和2类型两个三角形)
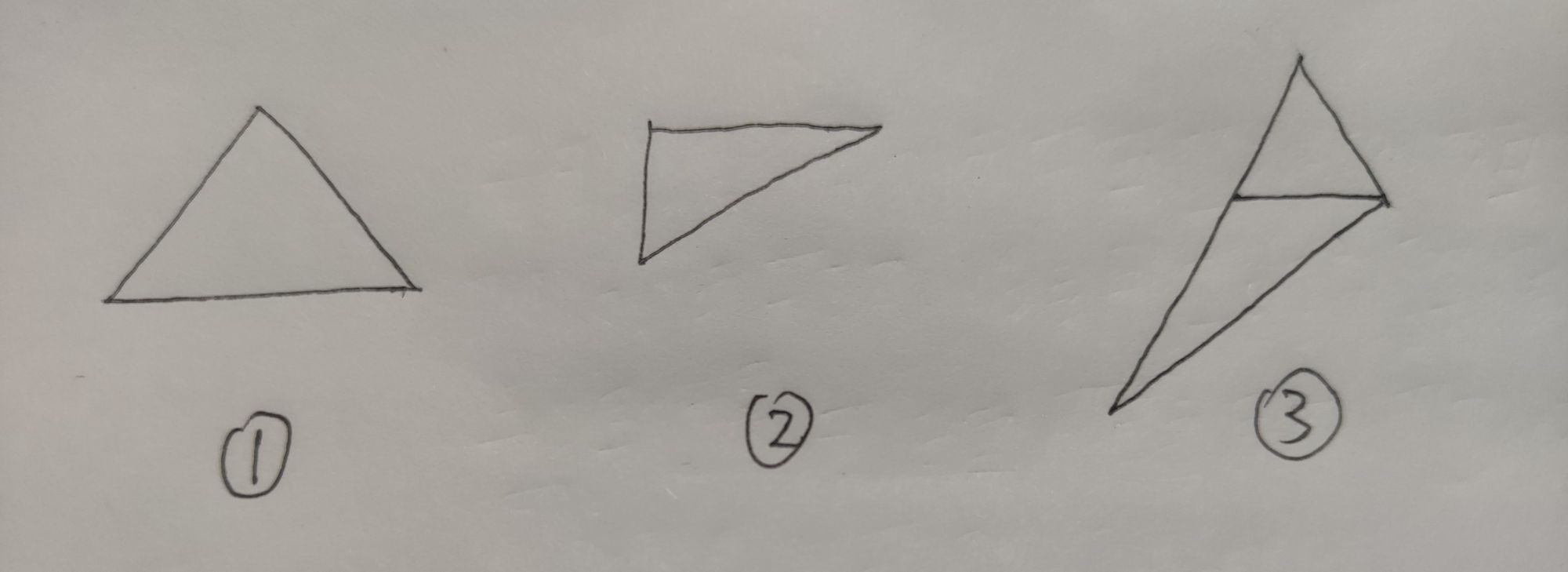
从而,我们可以知道,只要会画1和2这两类三角形,我们就可以通过组合,画出任意三角形!
接下来就介绍下如何画出第1类三角形。

第2类和第1类基本一样,就不写了,直接介绍最后的任意三角形绘制:
我们发现要想用画1和2类三角形的方法画任意三角形的时候,还缺了一个点,组成两个三角形。所以我们还需要确定第四个点v4的位置:
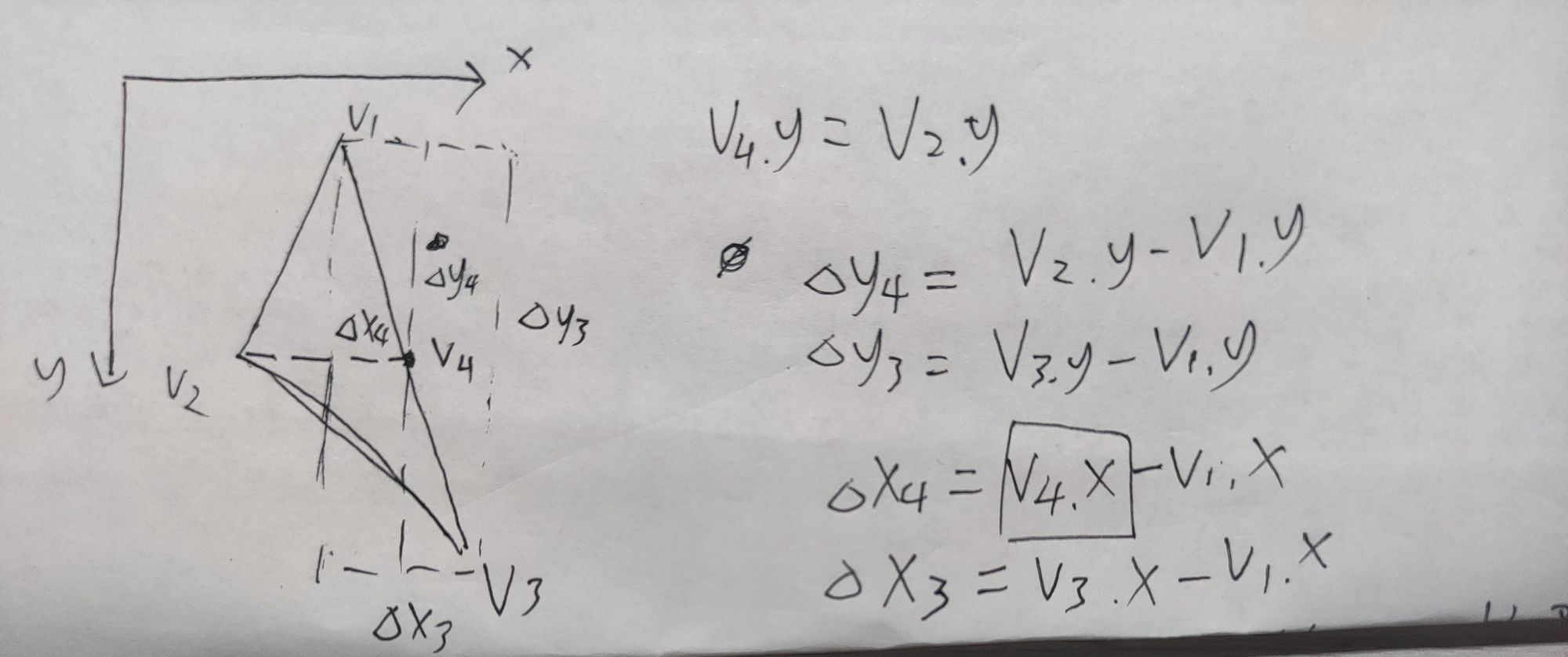
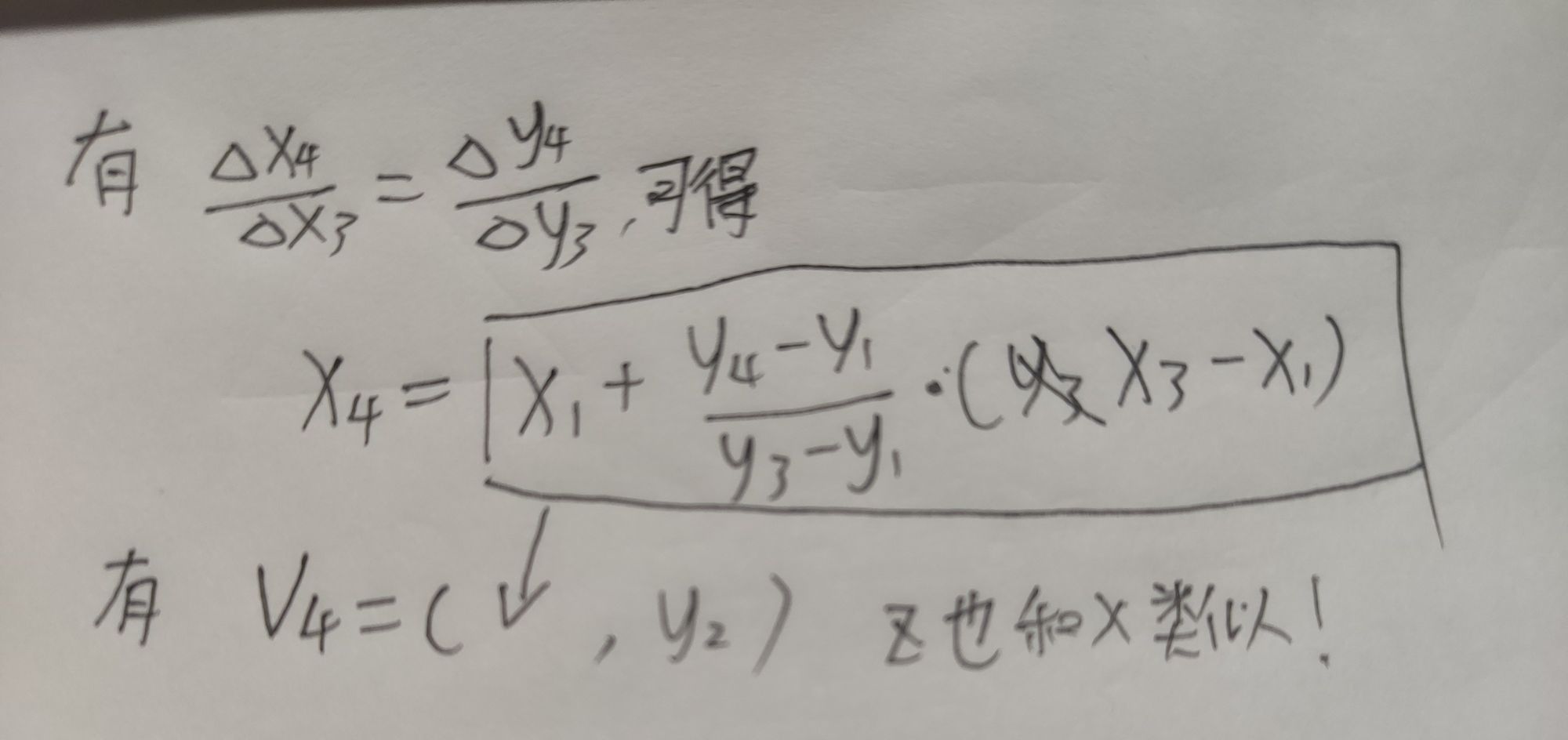
这里的证明都是初中几何知识,简单但是最好自己画一下。
得到了第4个点的坐标就可以用前面画1和2类三角形的函数画出整个三角形了!
void DrawTopFlatTriangle(const Vec& v1, const Vec& v2, const Vec& v3, const Color& color)
{
double XL = v1.x, XR = v1.x;
double dX1 = -(v2.x - v1.x) / (v2.y - v1.y), dX2 = -(v3.x - v1.x) / (v3.y - v1.y);
double ZL = v1.z, ZR = v1.z;
double dZ1 =- (v2.z - v1.z) / (v2.y - v1.y), dZ2 =- (v3.z - v1.z) / (v3.y - v1.y);
if (round(v1.y) - round(v2.y) <= 1) {
DrawScanLine(XL, ZL, XR, ZR, round(v1.y), color);
return;
}
for (int y =round( v1.y); y > v2.y; y--)
{
DrawScanLine(XL, ZL, XR, ZR, y, color);
XL += dX1;
XR += dX2;
ZL += dZ1;
ZR += dZ2;
}
}
void DrawBottomFlatTriangle(const Vec& v1, const Vec& v2, const Vec& v3, const Color& color)
{
double XL = v1.x, XR = v1.x;
double dX1 = (v2.x - v1.x) / (v2.y - v1.y), dX2 = (v3.x - v1.x) / (v3.y - v1.y);
double ZL = v1.z, ZR = v1.z;
double dZ1 = (v2.z - v1.z) / (v2.y - v1.y), dZ2 = (v3.z - v1.z) / (v3.y - v1.y);
if (round(v2.y) - round(v1.y) <= 1) {
DrawScanLine(XL, ZL, XR, ZR, round(v1.y), color);
return;
}
for (int y = round(v1.y); y <v2.y; y++)
{
DrawScanLine(XL, ZL, XR, ZR, y, color);
XL += dX1;
XR += dX2;
ZL += dZ1;
ZR += dZ2;
}
}
void DrawTriangle(const Vec& v1, const Vec& v2, const Vec& v3, const Color& color)
{
//按y值从小到大排序3个顶点
Vec V[3] = { v1,v2,v3 };
int maxIndex=0, minIndex = 0;
Vec maxV = v1, minV = v1,midV=v1;
for (int i = 0; i < 3; i++)
{
if (V[i].y < minV.y)
{
minIndex = i;
minV = V[i];
}
if (V[i].y > maxV.y)
{
maxIndex = i;
maxV = V[i];
}
}
int midIndex;
for (int i = 0; i < 3; i++) {
if (i == maxIndex || i == minIndex) {
continue;
}
else {
midIndex = i;
midV = V[i];
}
}
Vec V1 = minV, V2 = midV, V3 = maxV;
V1.x = (int)V1.x; V1.y = (int)V1.y;
V2.x = (int)V2.x; V2.y = (int)V2.y;
V3.x = (int)V3.x; V3.y = (int)V3.y;
if (V1.y == V2.y) {
DrawTopFlatTriangle(V3, V1, V2, color);
}
else if (V2.y == V3.y) {
DrawBottomFlatTriangle(V1, V3, V2, color);
}
else {
Vec V4;
V4.y = V2.y;
V4.x = V1.x + (V4.y - V1.y) / (V3.y - V1.y) * (V3.x - V1.x);
V4.z = V1.z + (V4.y - V1.y) / (V3.y - V1.y) * (V3.z - V1.z);
DrawBottomFlatTriangle(V1, V2, V4, color);
DrawScanLine(V2.x, V2.z, V4.x, V4.z, V2.y, color);
DrawTopFlatTriangle(V3, V2, V4, color);
}
}
下面附上用这个三角形光栅化算法画的兔子!
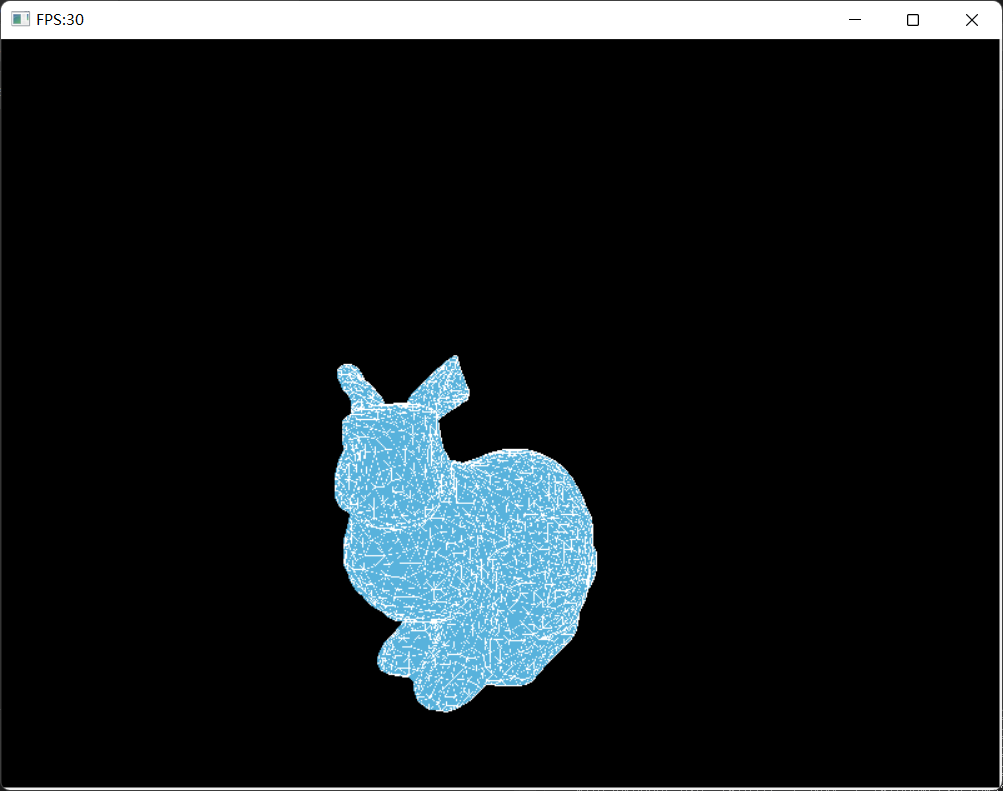
[3] 重心坐标(Barycentric Coordinates)
重心坐标这里是将三角形内的任意点p的坐标,用三角形的顶点坐标表示出来,形如:p=iA+jB+k*C。
这样三角形任意点的坐标都可以表示为(i,j,k),对于图形学中需要对三角形内用到插值的各种功能非常有用,如纹理贴图,光照等。
为了给mini3DRender加上纹理贴图功能,就必须需要先了解三角形重心坐标。
这个文章首先会介绍三角形重心坐标,最后通过重心坐标完成三角形内插值运算。
首先先介绍一下直线的重心坐标

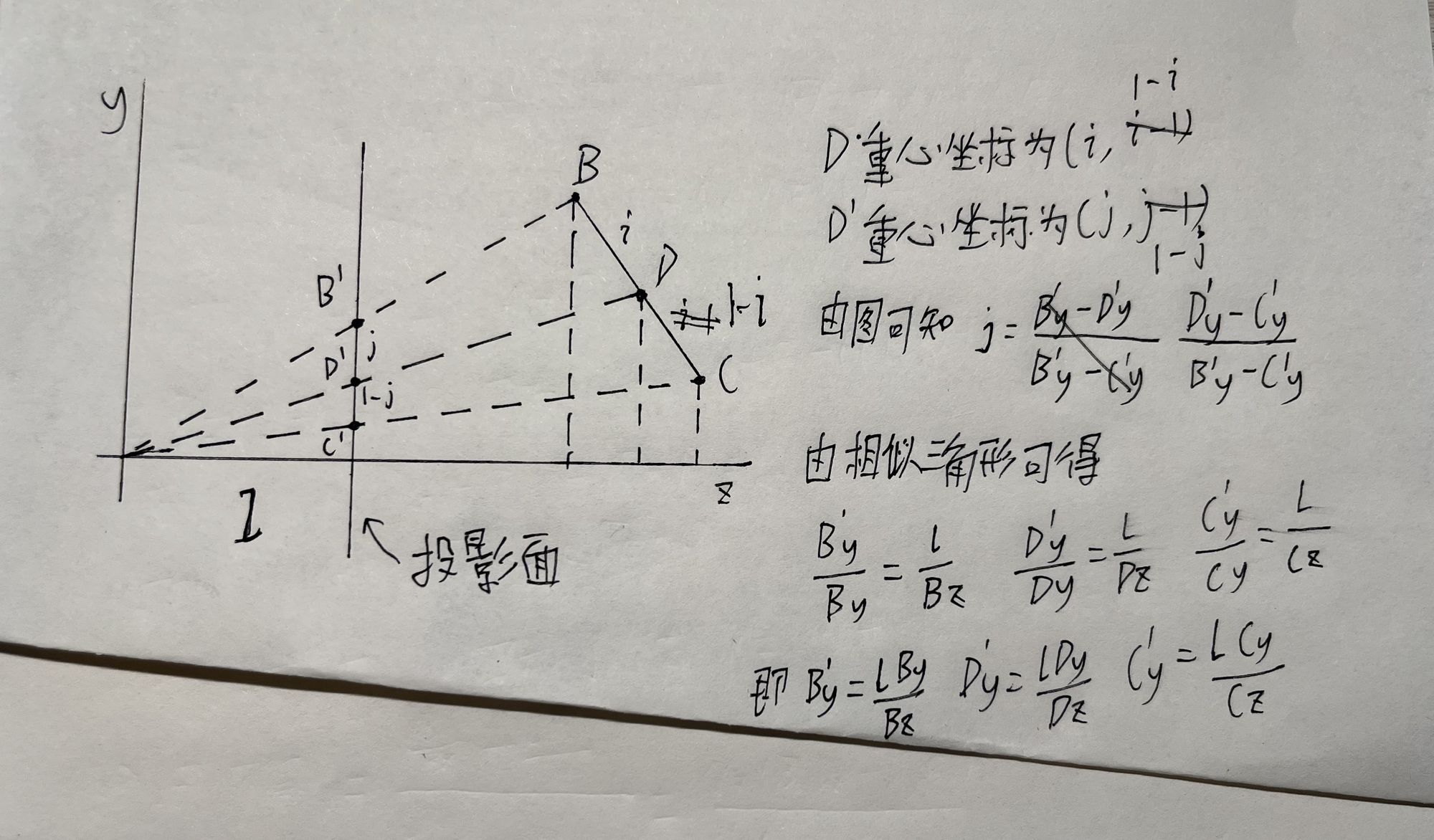
直线的重心坐标就是将在直线上的任意点用两个端点表示:p=jA+kB (j+k=1),我们用这个结论推一下三角形的任意点重心坐标表示。


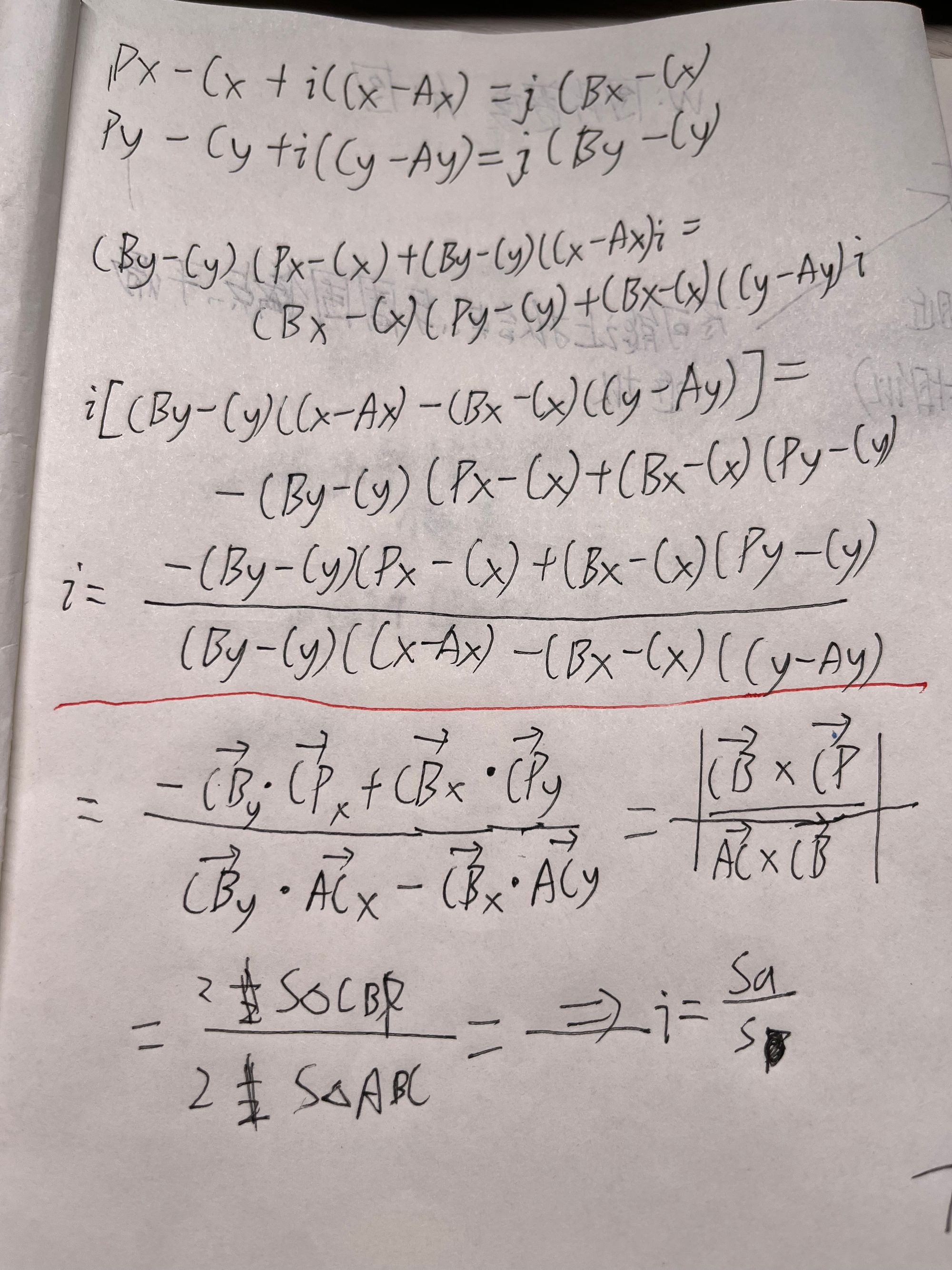
如上面两张草稿纸推的,我们可以得出任意点的重心坐标中的i,j,然后k就等于1-i-j。
于是我们就得到二维三角形内任意点的重心坐标。
但是,我的mini3DRender最后经过了透视投影,坐标发生了变换,我们这里计算的结果也要相应的修正。

参考链接
【GAMES101-现代计算机图形学课程笔记】Lecture 09 Shading 3 (纹理映射)
图形学基础知识:重心坐标(Barycentric Coordinates)
深入探索透视纹理映射(上)
深入探索透视纹理映射(下)
[4] 纹理映射关于透视投影的矫正
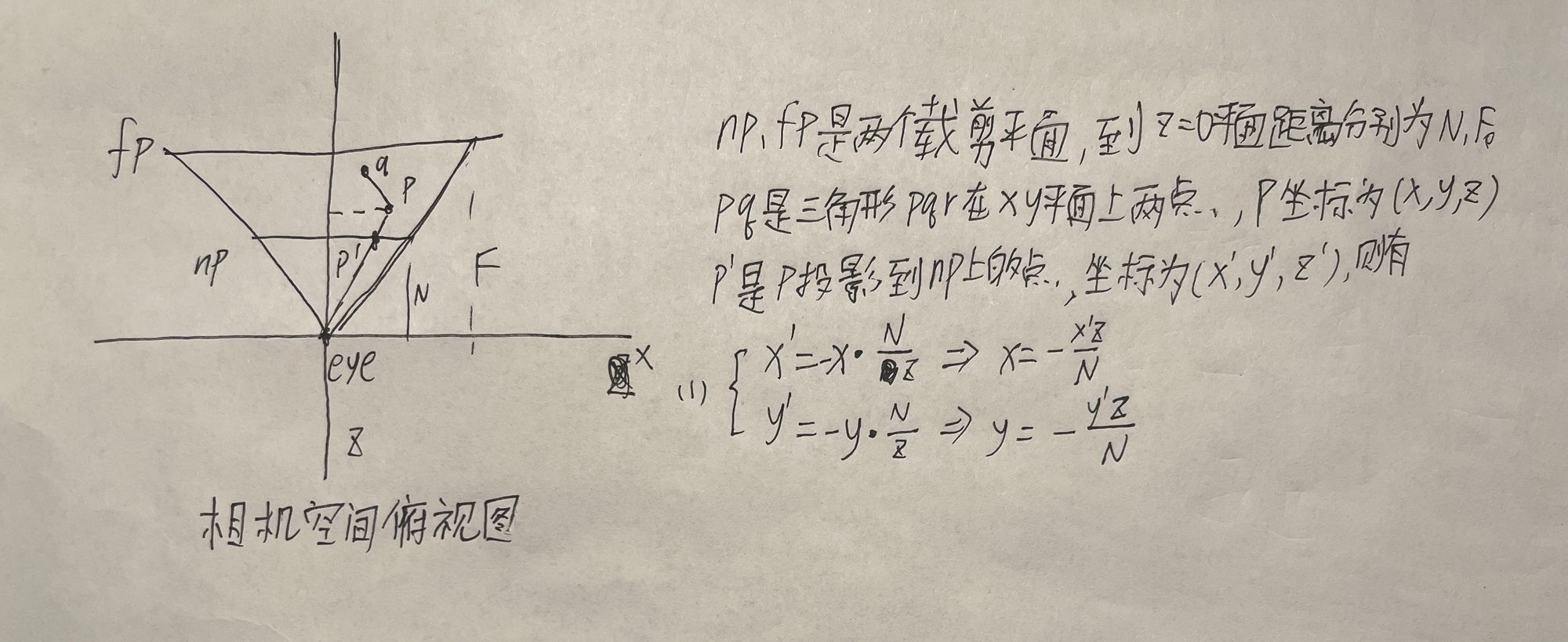
绘制三角形时需要贴图,贴图需要u、v坐标,u、v坐标需要插值,而相机空间坐标变换到裁剪空间并不能保持线性,整个空间扭曲了!(透视投影)
所以u、v坐标的插值不能用裁剪空间或者后面的屏幕空间(裁剪空间到屏幕空间的变换是线性的)的坐标进行插值,而要用相机空间的坐标来计算u、v插值。
这篇文章的目标是将裁剪空间的坐标还原为相机空间坐标。
这篇文章基本上是对深入探索透视纹理映射(上)和深入探索透视纹理映射(下)做的笔记。

[5] 光照
光照,在光栅化渲染器中,是使用近似方法表现类似自然界中的物体光照效果。
这里会介绍Blinn-Phong和Phong光照模型,基本步骤如下图所示:

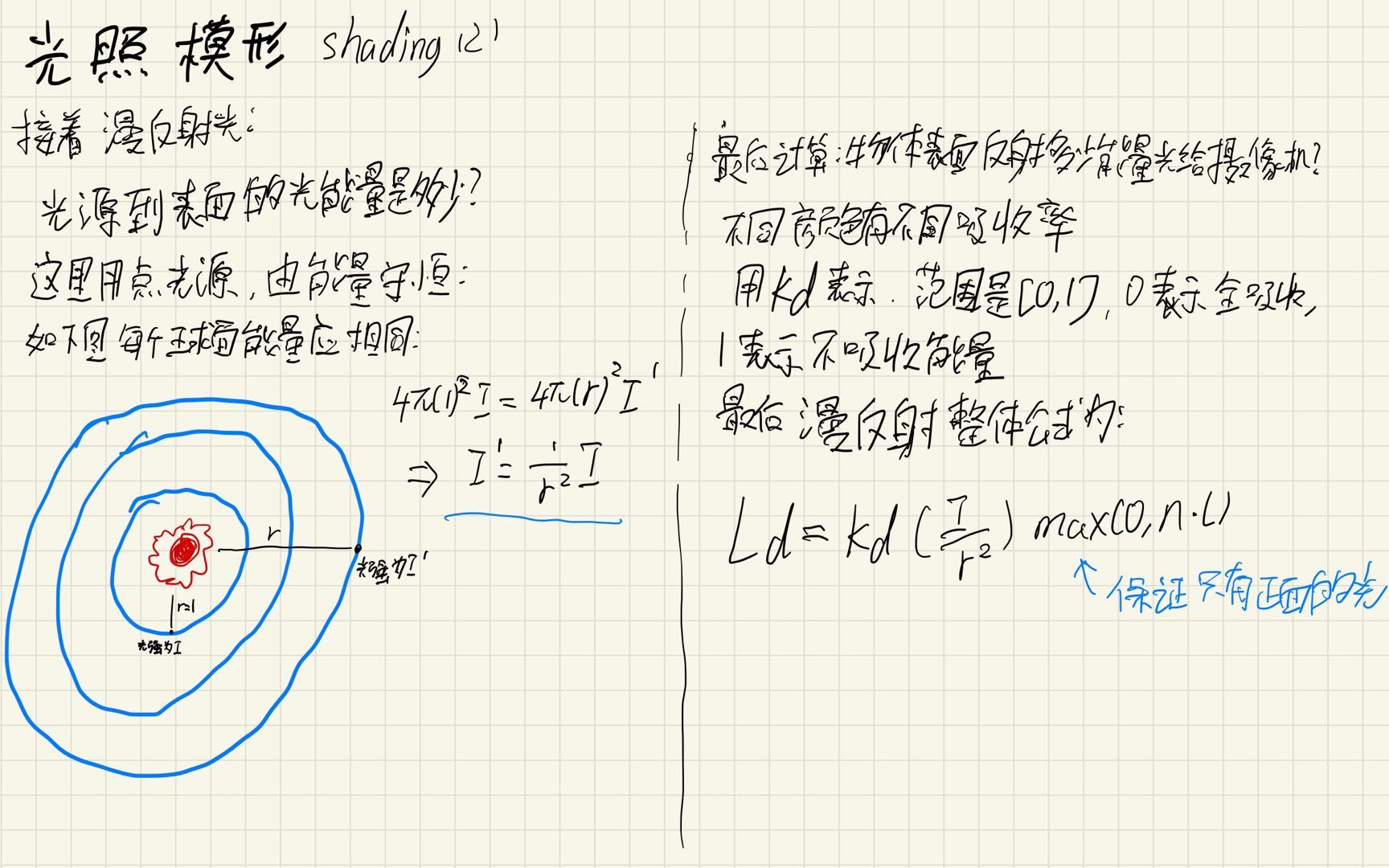
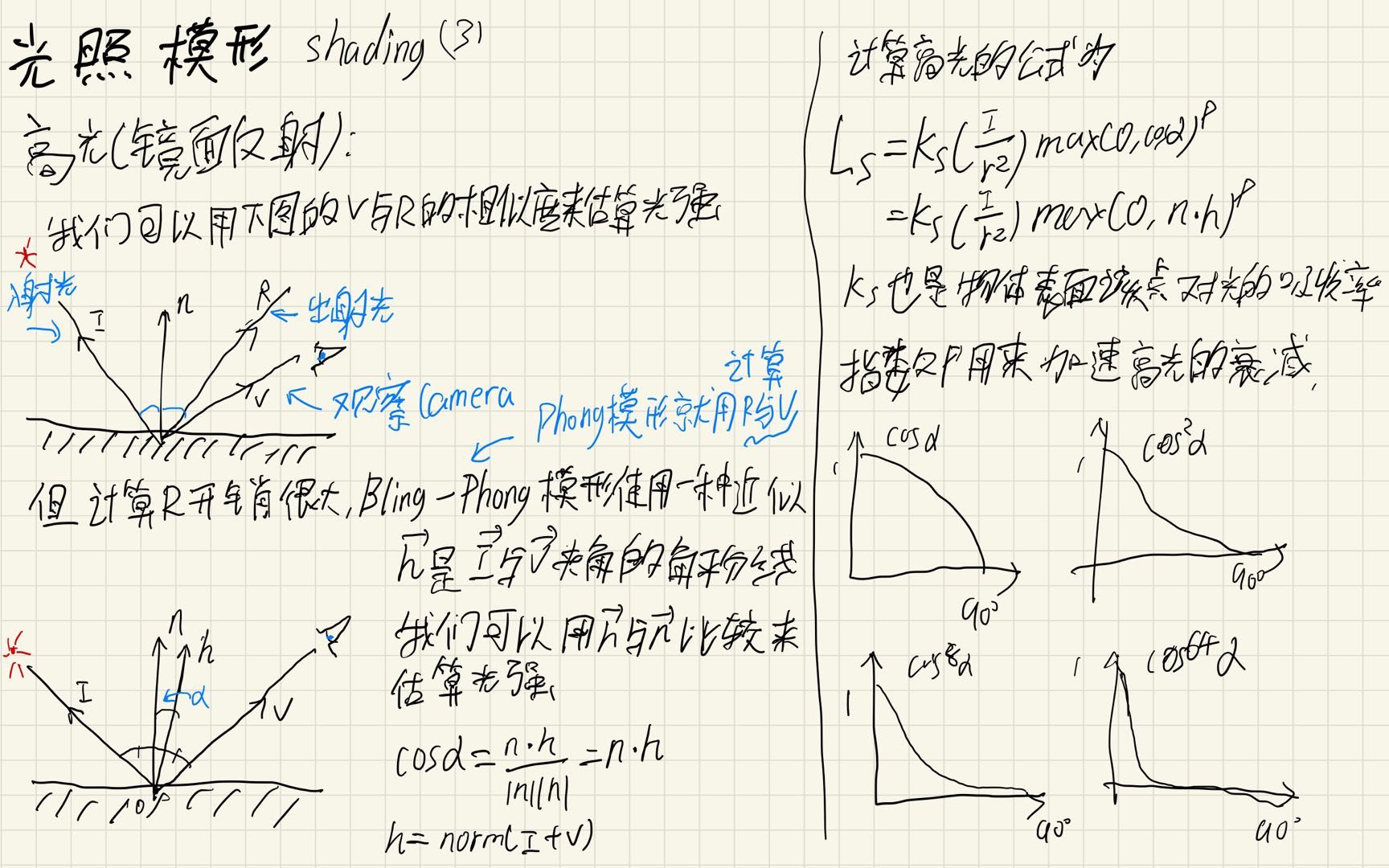
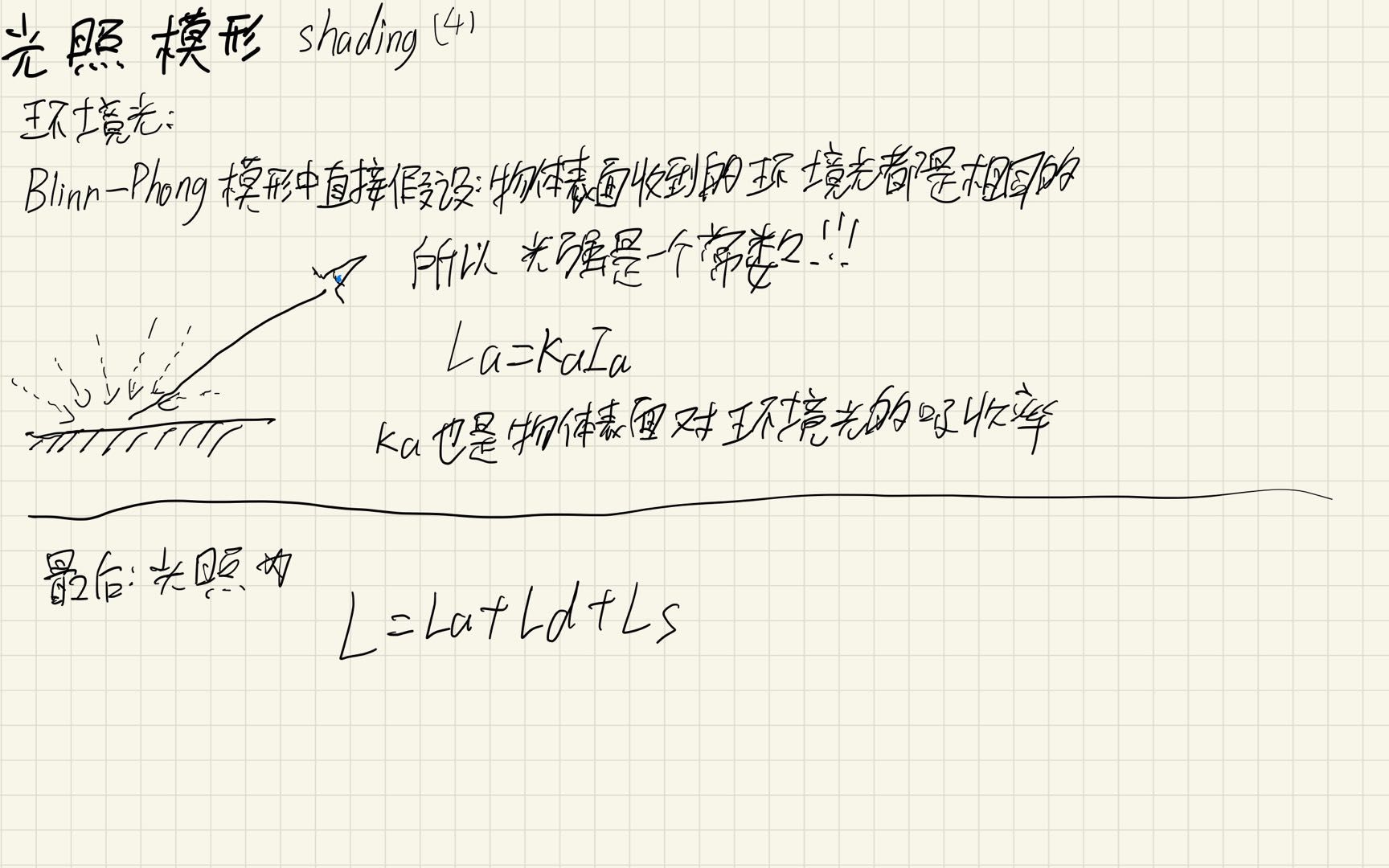
这两个模型将整体的光照分为:
Ambient(环境光)+Diffuse(散射光)+Specular(高光或镜面反射光)
原理

实现
我将会在mini3DRender里面添加光照功能。
- 新建light.h 和 light.cpp,对点光源进行定义
- 在绘制三角形函数中计算当前三角形的法向量,传入到最后的绘制扫描线函数
- 根据上面的公式计算,计算每个点的光照
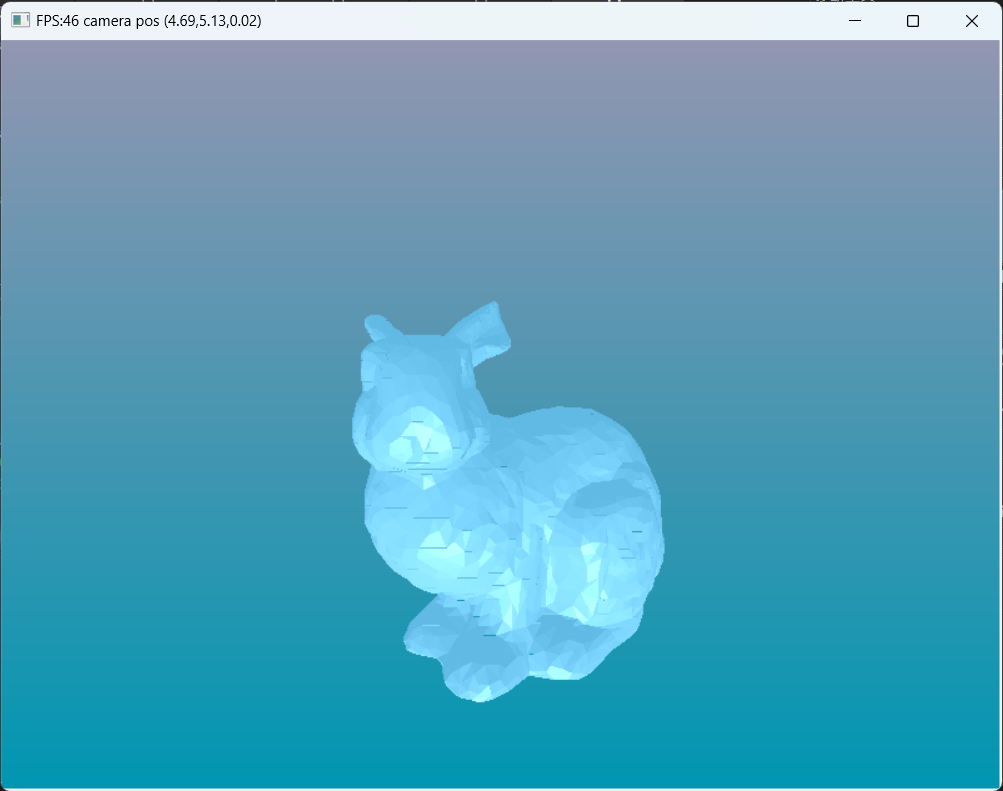
效果
下面还是斯坦福兔子!(但是加了光照)
参考
初学光栅渲染器的一些参考资料
入门Shading,详解Blinn-Phong和Phong光照模型
