背景
最优化方法是一门关于找凸函数的最值点的一系列方法,本文会介绍一些最优化方法的原理以及使用C++的实现。
代码在https://github.com/yufeiran/ConvexOptimization 中
目录
[1] 内点法(interior point method)
[2] 2d fused lasso
[3] Soft Thresholding
[4] Proximal gradient descent
[5] ADMM
[1] 内点法(interior point method)
主要参考这篇文章【学界/编码】凸优化算法 I: 内点法(interior point method)求解线性规划问题,根据自己的理解进行实现。
主要分为两部分:数学推导和C++实现
数学推导

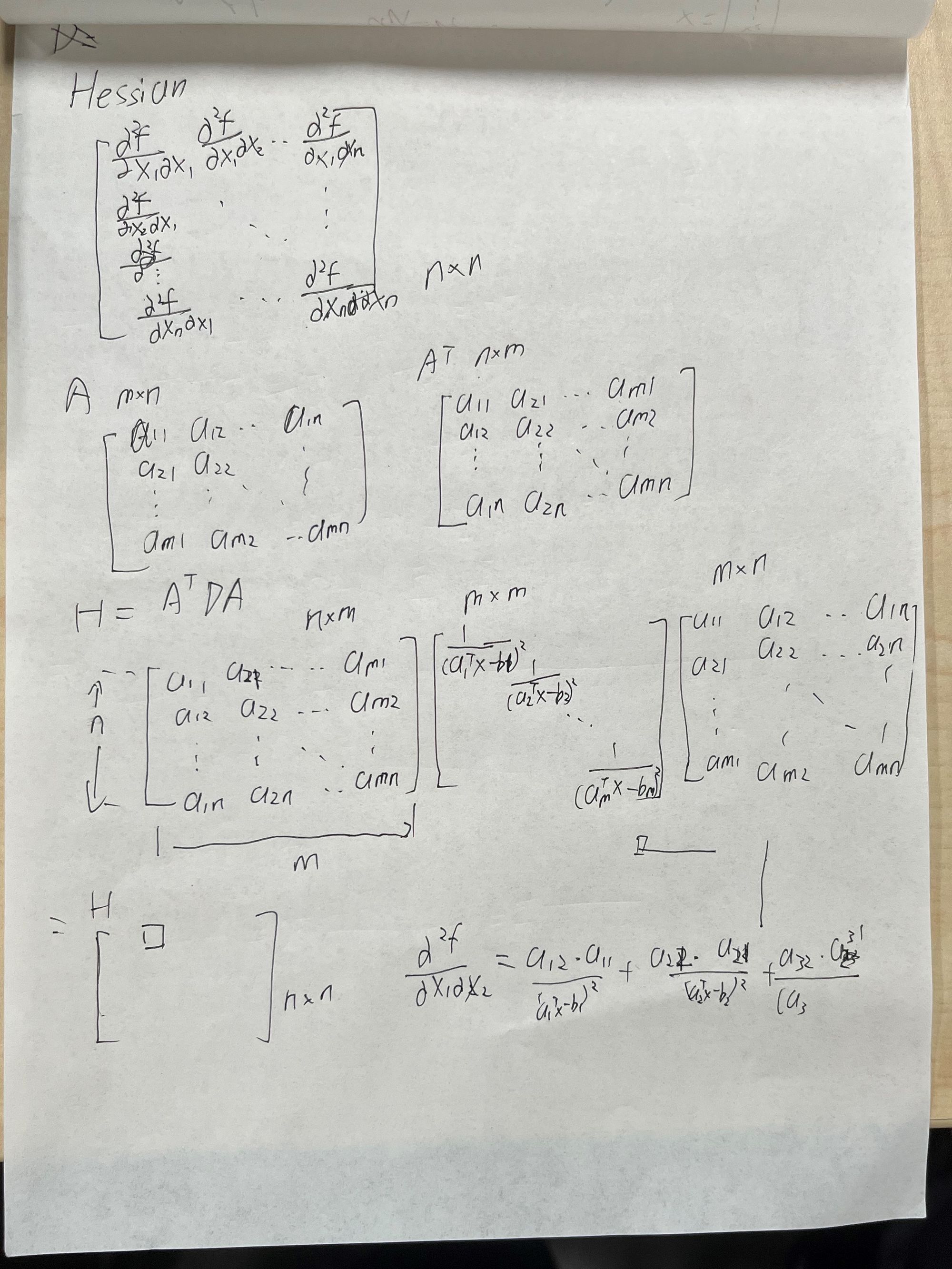

C++实现
实现一个可视化的内点法,主要结构由:向量矩阵运算库、可视化框架和内点法算法组成。
1.向量矩阵运算库
至少需要支持矩阵和向量的乘法
2.可视化框架
这里使用之前写的miniEngine2D
3.内点法算法
根据前面的推导实现算法
完整代码在ConvexOptimization/InteriorPointMethod/中
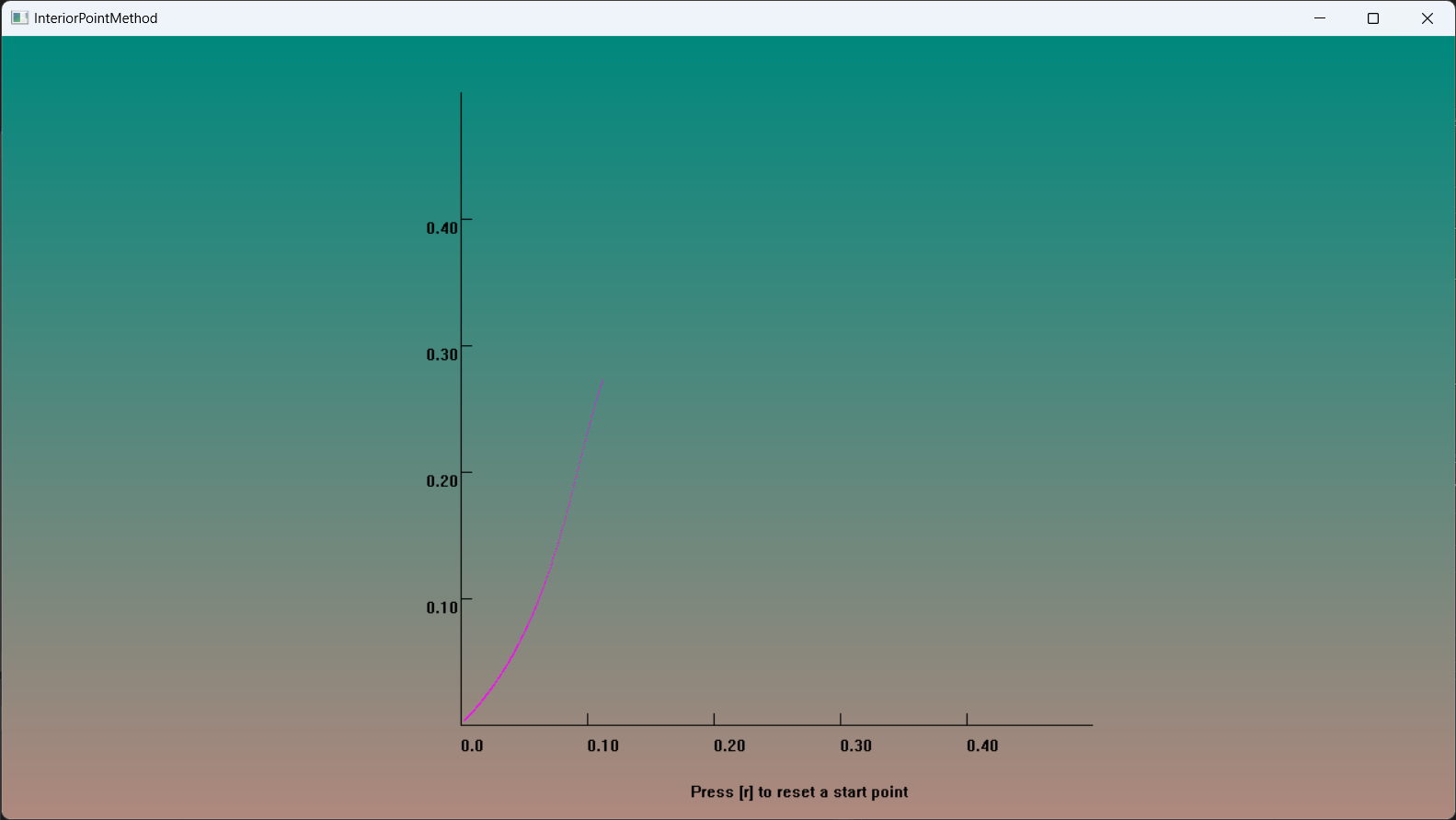
运行结果
用内点法计算该线性规划问题,如图所示,绝大部分点都可以收敛到(0,0)
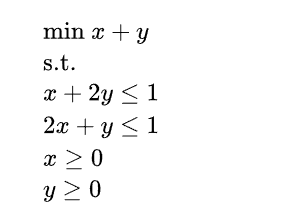
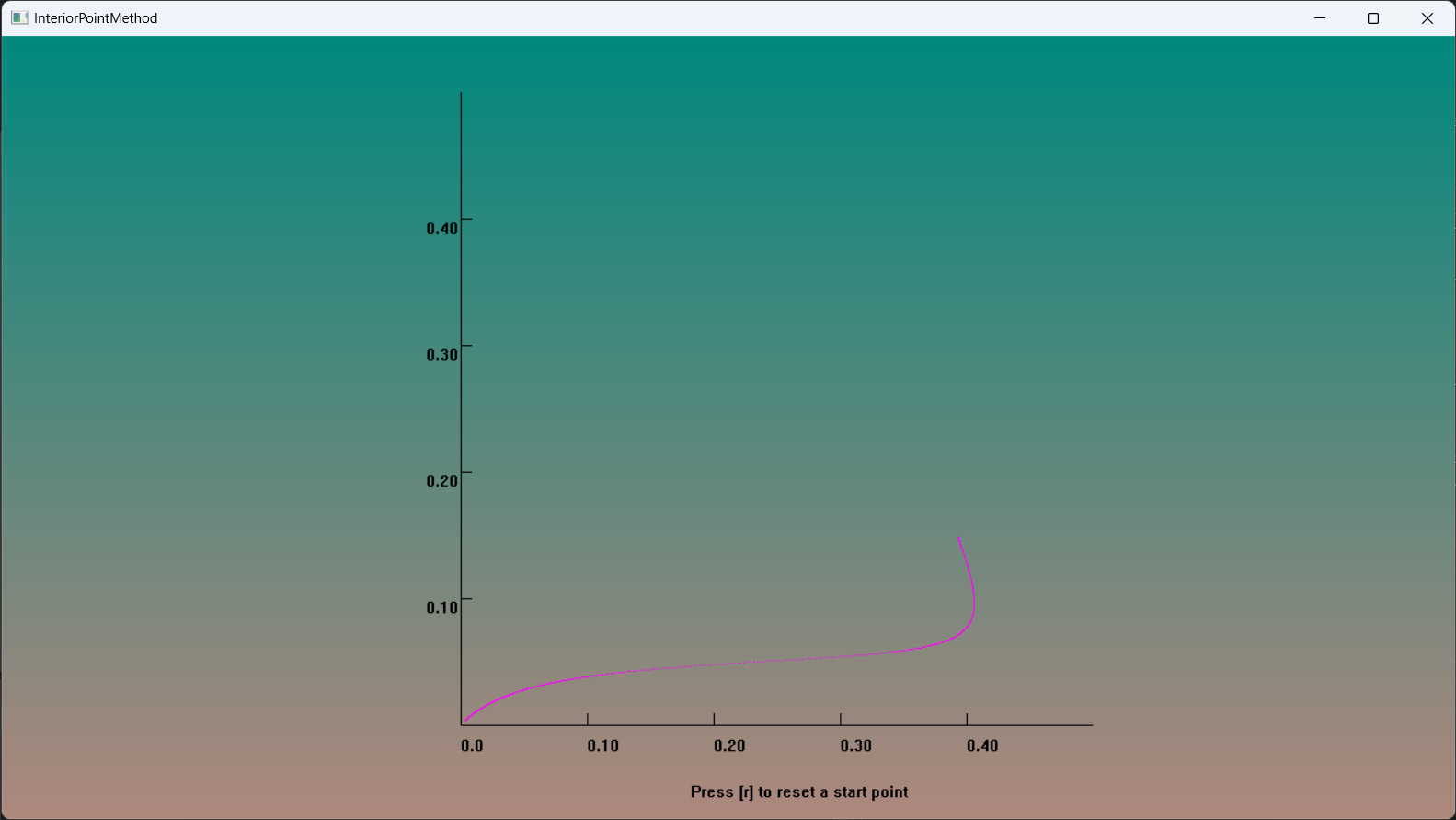
[2] 2d fused lasso
背景
最优化,是应用数学的一个分支。主要研究在特定情况下最大化或最小化某一特定函数或变量。
通过C++实现经典代码有助于深入理解其数学原理。今天先来实现一个基础的最优化算法2d fused lasso
2d fused lasso
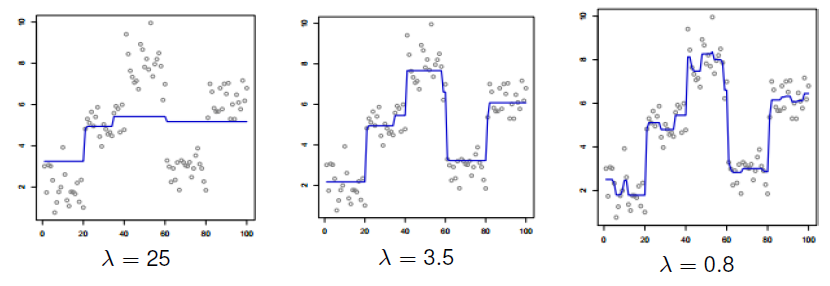
目标如下图所示,通过这个2d fused lasso算法,可以将加了噪声的图像尽量的复原。

参考链接
【学界/编码】凸优化算法 I: 内点法(interior point method)求解线性规划问题
判定(半)正定矩阵的特殊大于(等于)简写符号
Sparse fused lasso tutorial
Lasso 稀疏约束 + Group Lasso 分组最小角回归算法
[3] Soft Thresholding
Soft Thresholding是一个非常常见的函数,这里我根据下面这篇文章自己写了一个笔记。
软阈值(Soft Thresholding)函数解读



[4] Proximal gradient descent
背景
近似梯度法 (Proximal gradient method)是一种广义投影形式,用于解决不可微的凸优化问题。这样就可以使得很多问题能够用梯度下降法解出来。
内容


ps:零范数是所有非0元素数量 一范数是所有元素绝对值之和 二范数是所有元素平方之和的开方
公式中的二范数是矩阵二范数,可以看成形如AT*A 的形式,这里注意一下倒数第二行变到倒数第一行,它这个不是直接等于的,看我下面写的把最后一行那个二范数平方打开:
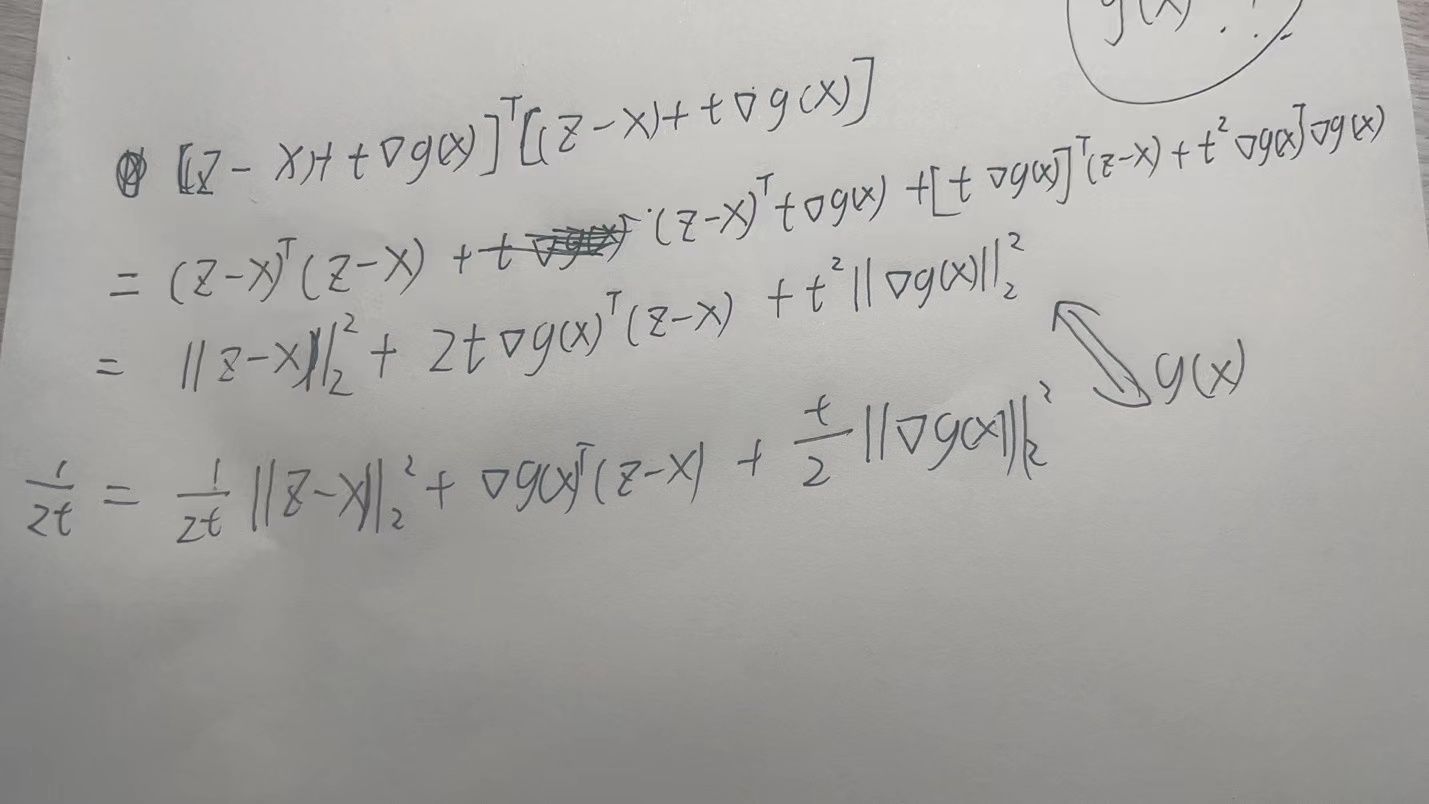
它们实际上不相等,但是,整个式子关心的是对z求最小值,其余的元素都看作常数,对常数加减不影响z取多少时整个式子最小!所以我们可以将配不上的最后一项直接改成g(x),这样就能得到二阶展开的式子。
将上面最后一行的式子用proxt(x)替换,我们可以得到一个迭代公式!用这个迭代公式就能不断迭代出解。

下图是一个标准的lasso例子,它的Prox Mapping如图所示:

根据最优化算法学习-Soft Thresholding这里的介绍,我们发现lasso 的Prox Mapping刚好等于soft-thresholding 算子!于是我们可以得到一个用soft-thresholding的迭代公式:

不需要求矩阵的逆!
[5] ADMM
背景
Alternating Direction Method of Multipliers(ADMM)是这门课老师说的对我们最重要的算法,所以需要特别掌握。
计划使用ADMM算法解决1d Fused LASSO问题。
内容
这个写的最好凸优化|笔记整理(B)——再看交替方向乘子法(ADMM),Frank-Wolfe方法
ADMM优化算法(附MATLAB代码)
分布式计算、统计学习与ADMM算法
下面是我自己做的笔记:

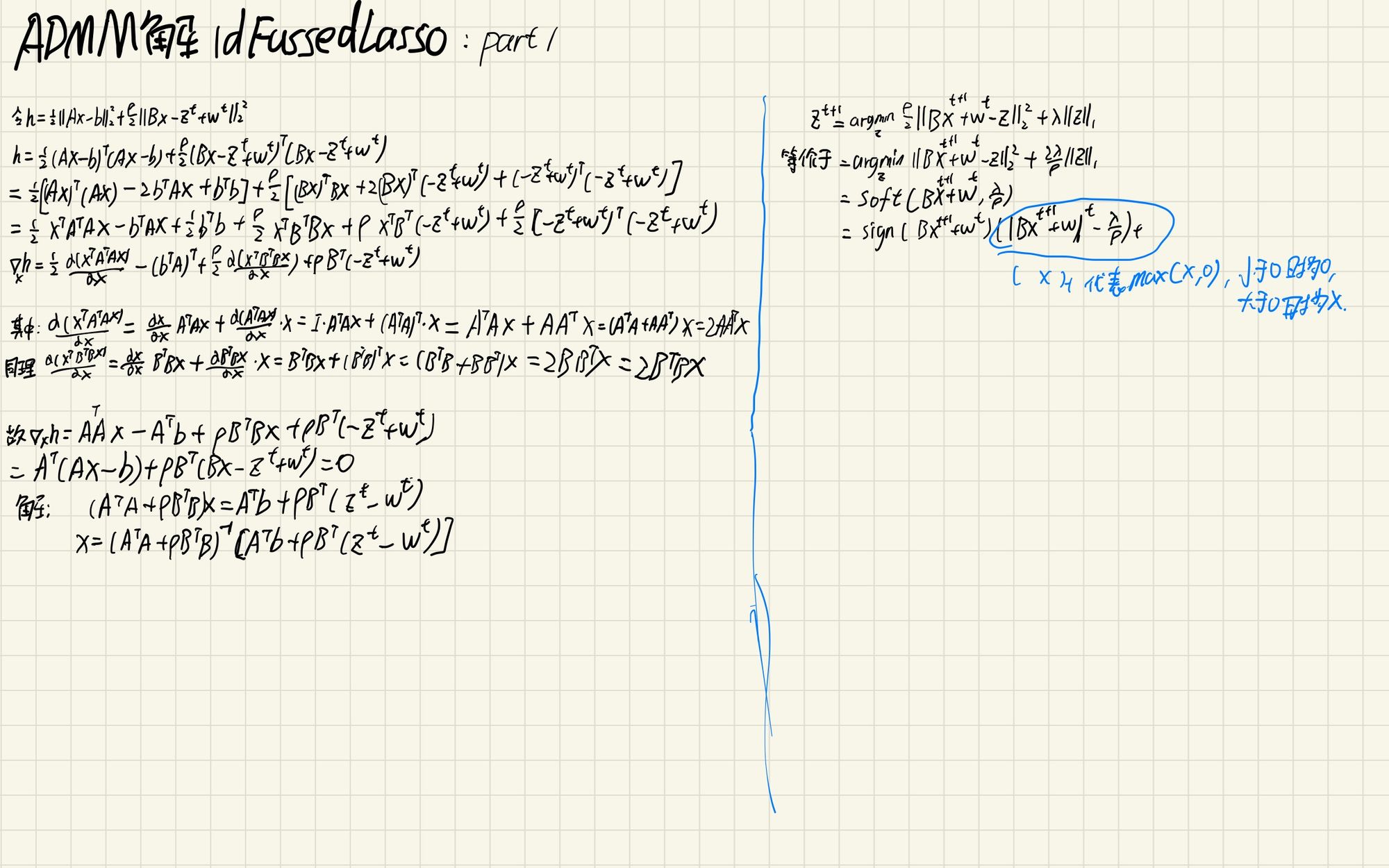
C++实现
实现代码链接:
https://github.com/yufeiran/ConvexOptimization/tree/main/ConvexOptimization/1dFussedLassoUseADMM
实现效果
ρ取0.3,λ取0.3时的效果如下图所示,虽然可以拟合一个比较平滑的曲线,但是对比课件中的算法感觉还是有差距,我推测是由于我的数值计算没有经过特殊处理,全都是用C++的double默认计算。
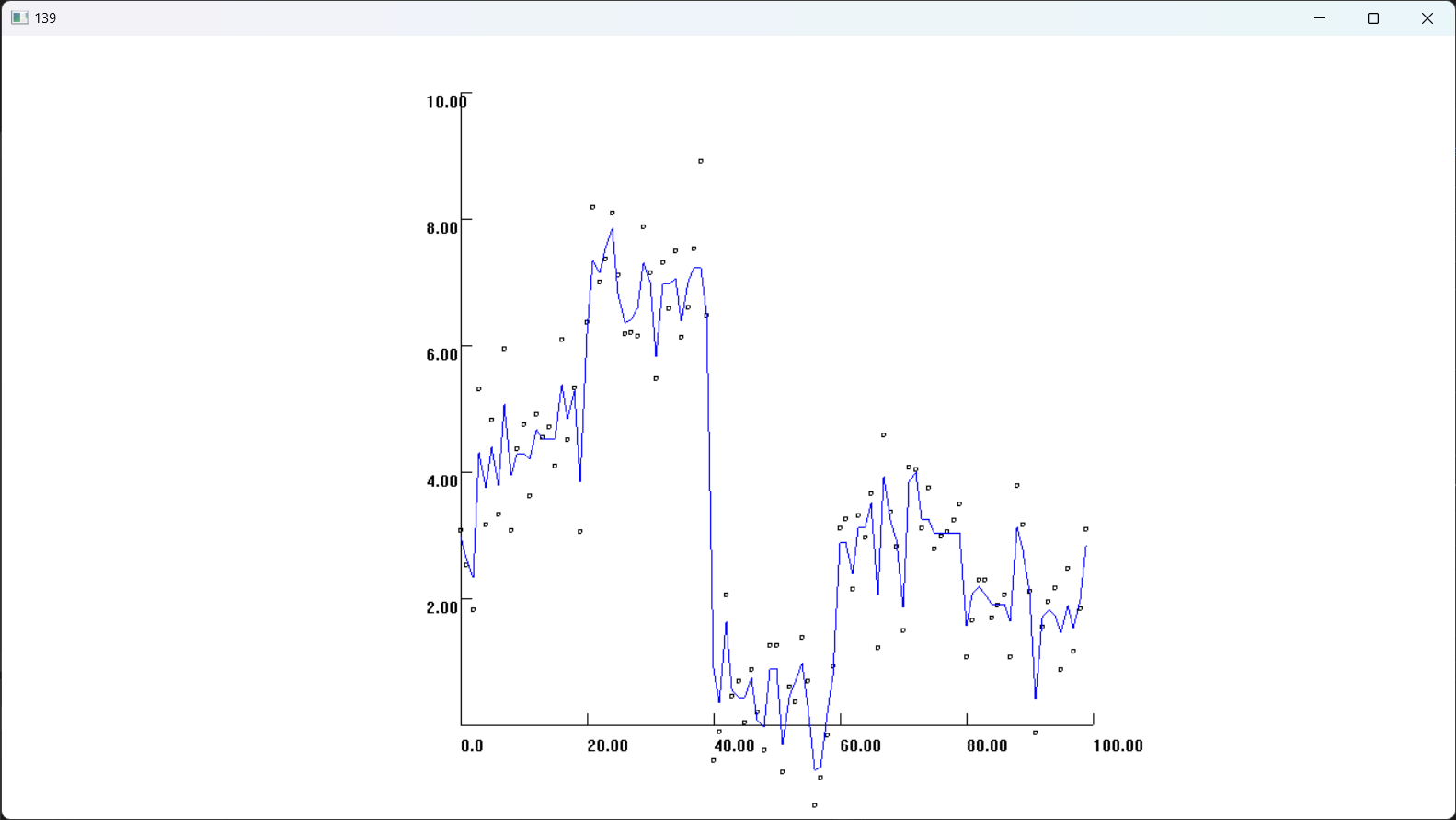
课件中的效果: