0. 背景
图形学坐标变换是将模型三维空间坐标变换成二维平面坐标的过程。光栅化/光线追踪渲染器都依靠该变换实现。掌握坐标变换是理解图形学渲染过程的基础。
我此前也实现过几个光栅化渲染器 (甚至在FPGA上实现过简单的),但是主要都是实现代码为主,看到数学推导部分就畏惧的跳过,对于这个坐标变换一直做不到心中有数。
所以为了扎实图形学基础,我便乘这个假期,准备在草稿纸上手推一遍整个过程,并尽力做到好理解。
在这个数学推导完成后会出相应的一个光栅化渲染器,争取基本手写。
1. 概要内容
整个坐标变换流程主要由以下四部分矩阵变换构成
- 三维齐次坐标和三维坐标的平移与旋转
- 物体空间(object space)到世界空间(world space)变换矩阵
- 世界空间(world space)到相机空间(camera space)变换矩阵
- 相机空间(camera space)到投影空间(clip space)也叫做 齐次裁剪空间(homogeneous clip space)变换矩阵
- 投影空间(clip space)到屏幕空间(screen space)变换矩阵
*如果你觉得对线性代数缺乏一些理解可以先看看3Blue1Brown出的线性代数的本质这门小课,理解到矩阵是一种空间变换这样的程度就可以了。
2. 推导过程
2.1 三维齐次坐标和三维坐标的平移与旋转
变换到世界空间以及变换到相机空间的操作本质上就是三维空间上的点平移和旋转的过程,所以先介绍一下平移矩阵和旋转矩阵以及平移操作需要的齐次坐标。这部分较为简单。
2.1.1 三维齐次坐标
三维齐次坐标的意思是在原本三维向量的基础上再加上一维,变成(x,y,z,w)四个维度。之所以要加入这一维,是因为三维方阵乘以三维向量的话,只能对三维向量进行缩放和旋转操作。为了能够进行平移变换操作,需要加入齐次坐标w。
2.1.2 三维坐标平移矩阵
原坐标为(x,y,z,1)T ,如图所示,左乘一个平移矩阵之后就可以实现平移变换
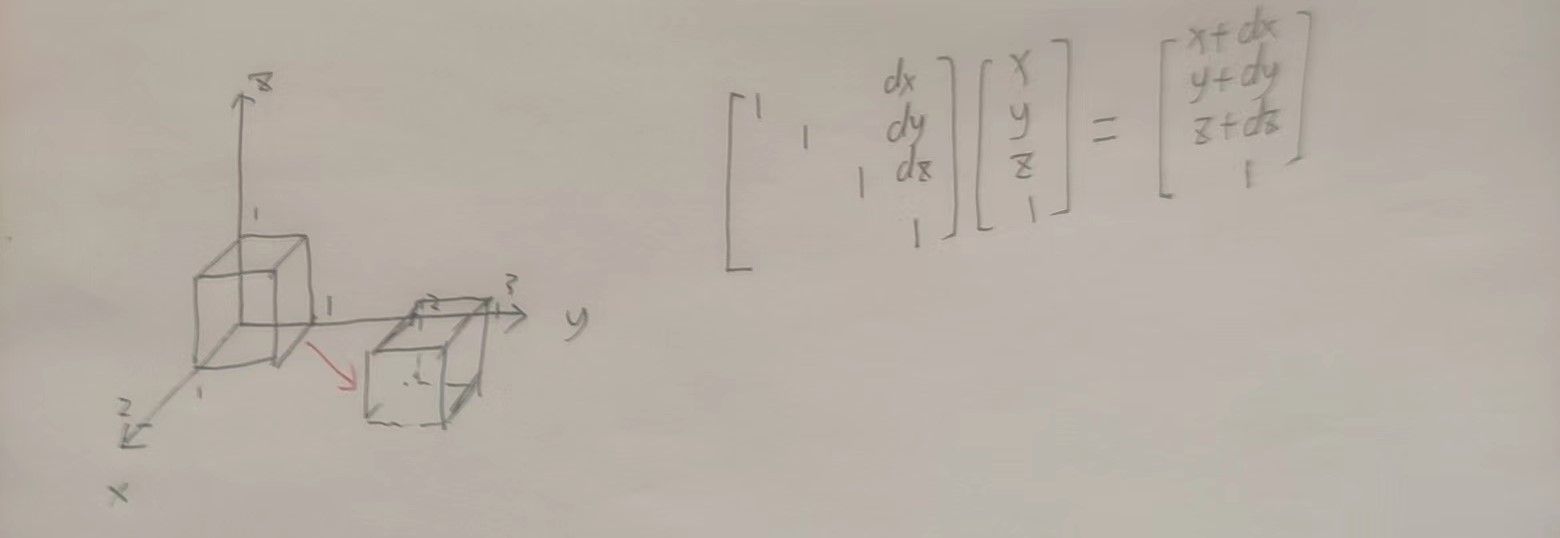
2.1.3 三维坐标旋转矩阵
如左图右手系三维标准坐标系所示,围绕某个轴旋转固定角度的矩阵如下,需要注意旋转的方向!
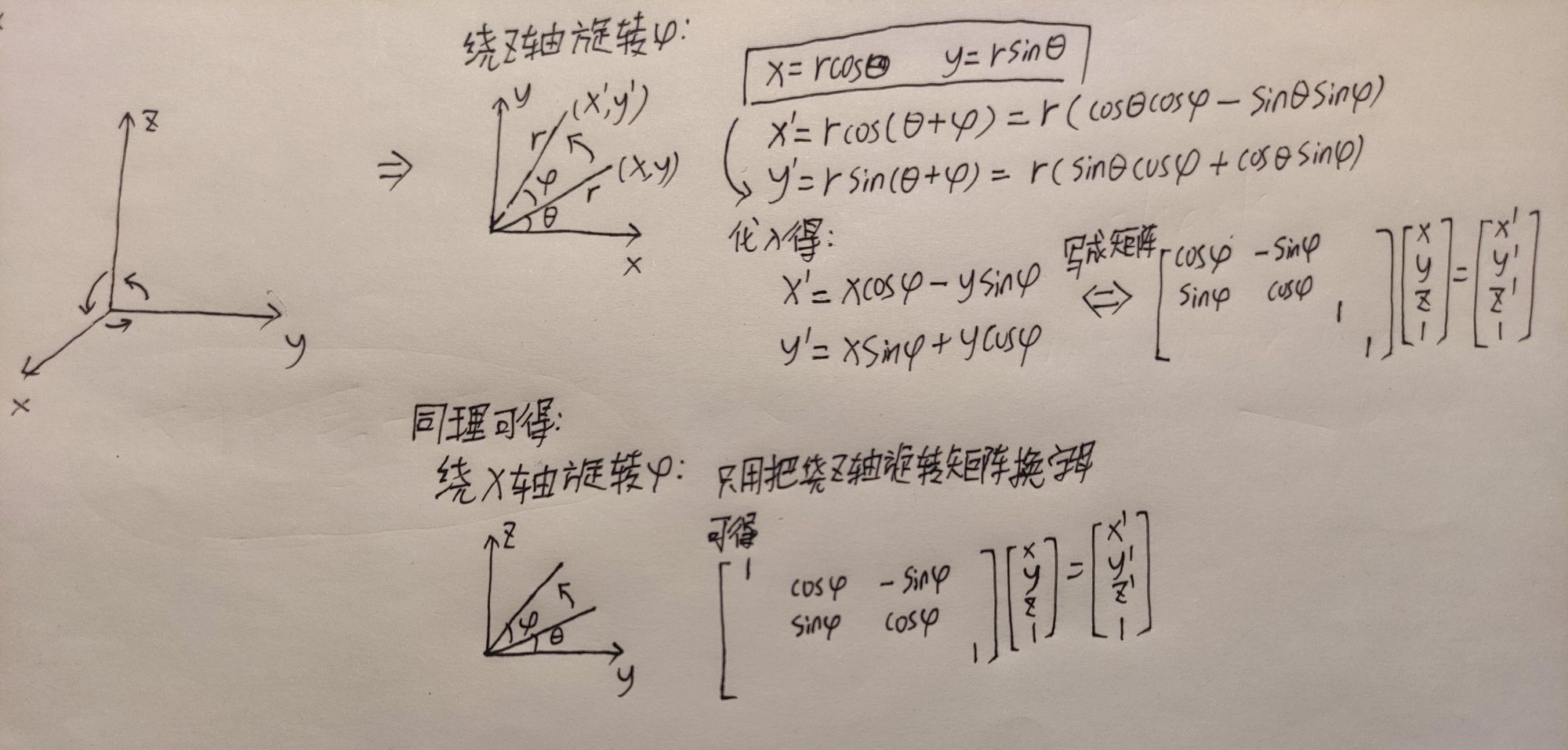
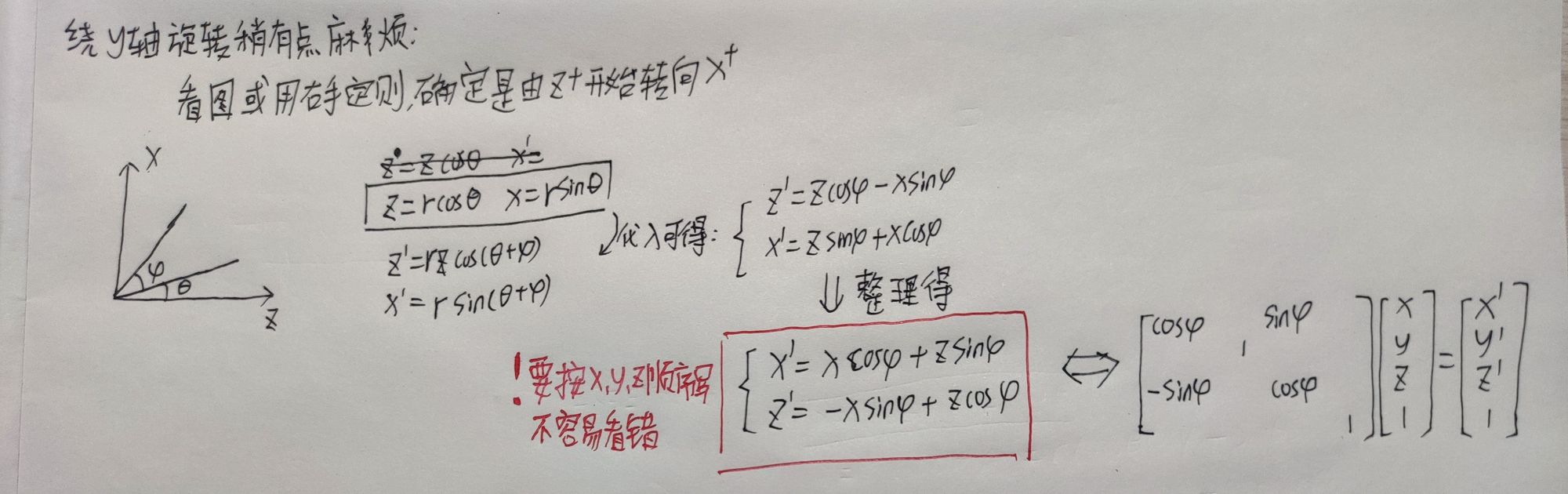
*由于坐标变成了四维,为了便于计算机实现,原本只需要3x3的旋转矩阵变成4x4的矩阵
2.1.4 三维坐标缩放矩阵
缩放矩阵就比较简单了,如下图所示
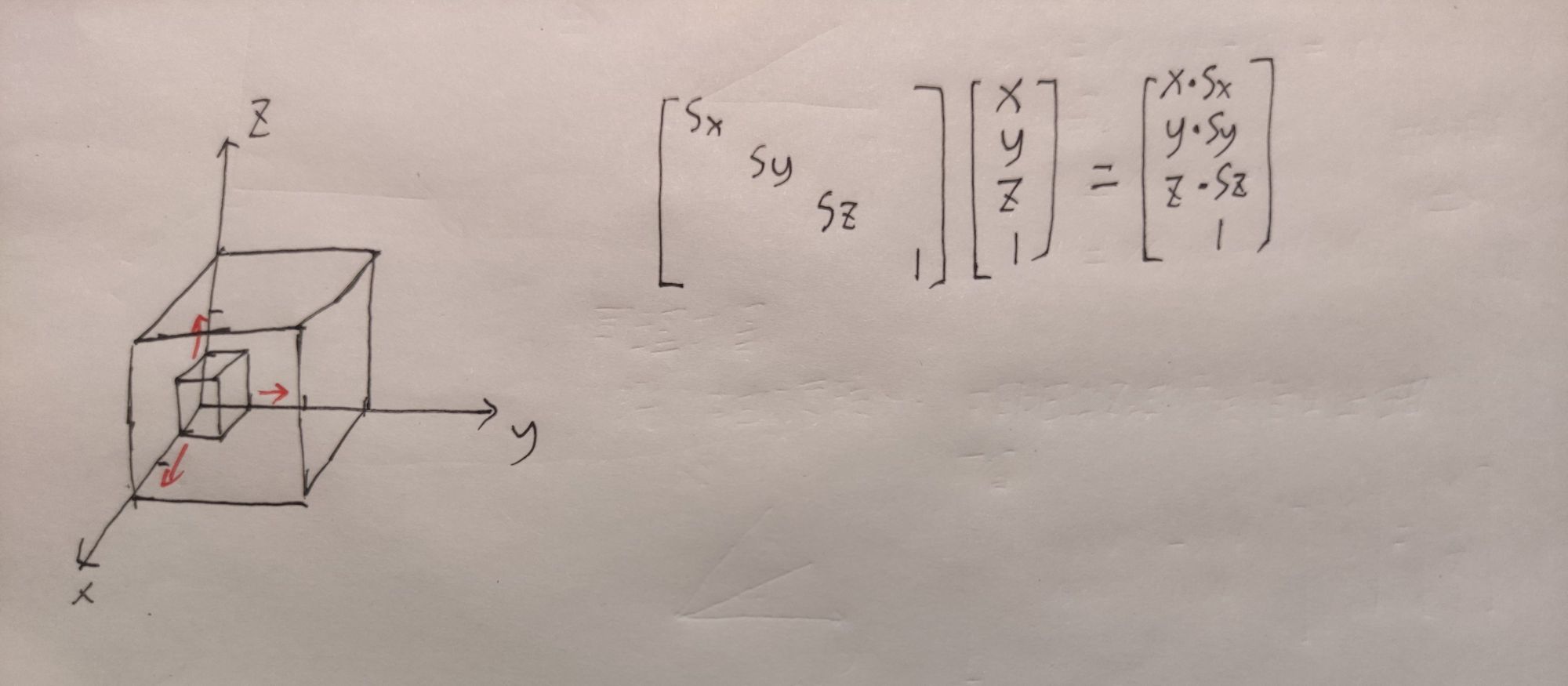
2.2 物体空间到世界空间矩阵
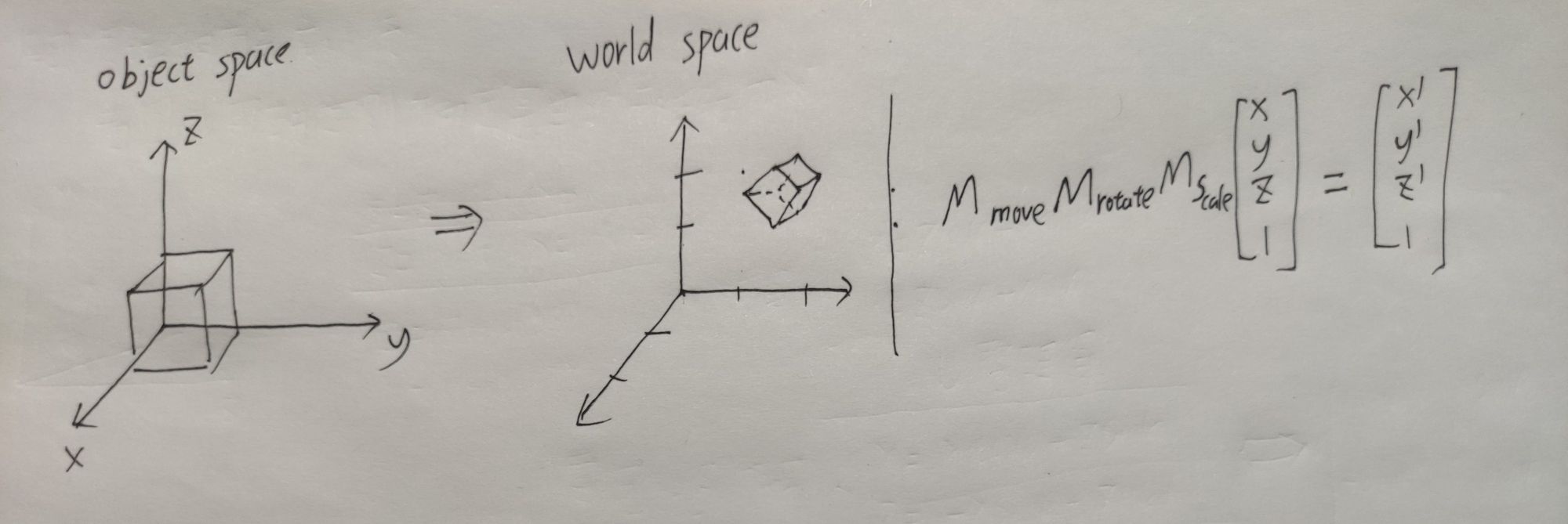
物体空间中的坐标左乘2.1节介绍的平移、旋转和缩放操作矩阵,就可以将在物体空间中的坐标转换到世界坐标系中,这一步骤比较好理解。
需要注意的是像我这里这样把向量竖着写,则变换矩阵需要左乘向量,并且计算顺序是从右到左,图中就是先缩放再旋转再平移。
2.3 世界空间到相机空间
世界到相机空间(也可以叫观察者空间)的变换由两步组成:
- 确定相机空间基向量
- 求解世界空间到相机空间的变换矩阵
2.3.1 确定相机空间坐标基
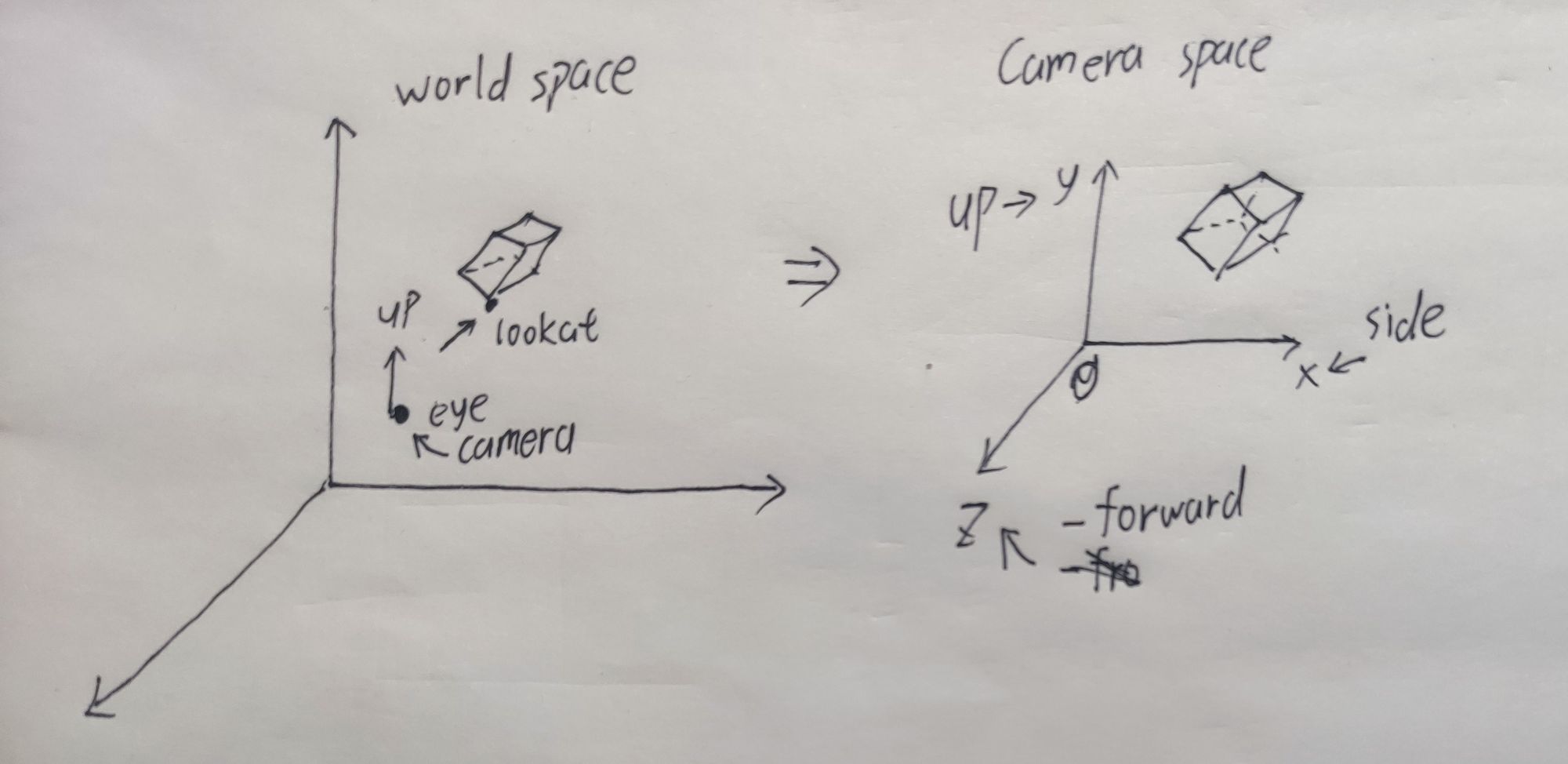
如上图所示,要在3维空间中放置一台相机,我们需要知道它的位置eye向量,它镜头看向的点lookat向量,以及相机本身的姿态(这里用up向量指示相机头顶指向的方向,up一般可以先给个初始值(0,1,0))。我们需要用这相机的三个向量求出相机空间坐标系(或者叫做u-v-n坐标系),以下是计算步骤:
-
求得相机指向的方向forward=lookat-eye,注意我们需要的是一组基向量,需要归一化:forward=forward/|forward|
-
我们求相机的side向量:我们先将up向量归一化,up=up/|up|。side=cross(forward,up)。这样就得到了一个垂直于up和forward的向量side。由于up和forward已经归一化了,所以side已经是单位向量了。
-
再确定up,up=cross(side,forward)。
为什么这里还需要再算一次up向量呢?是因为一开始给的up向量只指示了一个大致的方向,大部分情况下并不垂直于side和forward张成的平面。
我们现在就得到了三个互相垂直并且都是长度为1的向量,可以构成一个左手坐标系,但是整个坐标变换都在用右手坐标系,所以为了统一不容易出错将,其改成右手坐标系,即用-forward、side、up三个向量组成右手坐标系(原点在eye),也就是我们最终得到的相机空间基向量。
2.3.2 求解世界空间到相机空间的变换矩阵
要从世界空间坐标变换到相机空间,需要两个步骤:
- 将世界空间坐标系旋转到相机空间坐标系
- 将原点移到相机的位置eye
下图是位移矩阵和旋转矩阵,世界空间坐标变换到相机空间矩阵等于 Mmove*Mrotate
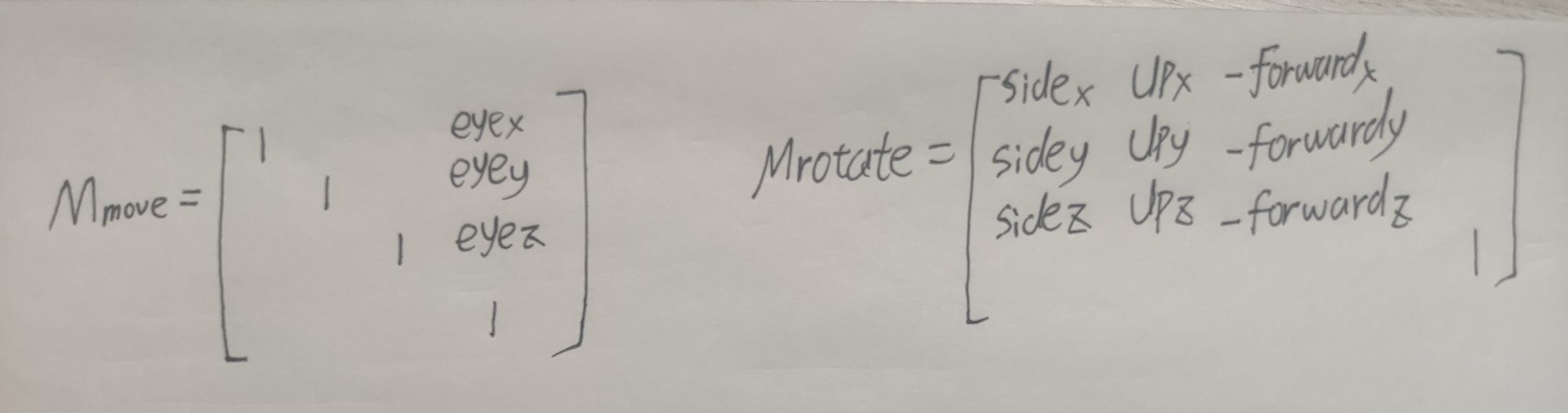
我们这里已知的是在世界坐标系中的坐标,我们想要求得的是这个世界坐标系中的坐标在相机空间坐标系中的坐标。所以我们需要的是一个从相机空间变换到世界空间的矩阵,也就是世界空间坐标变换到相机空间矩阵的逆矩阵,最终得出的矩阵如下图所示,把矩阵看出坐标变换会好理解一些。
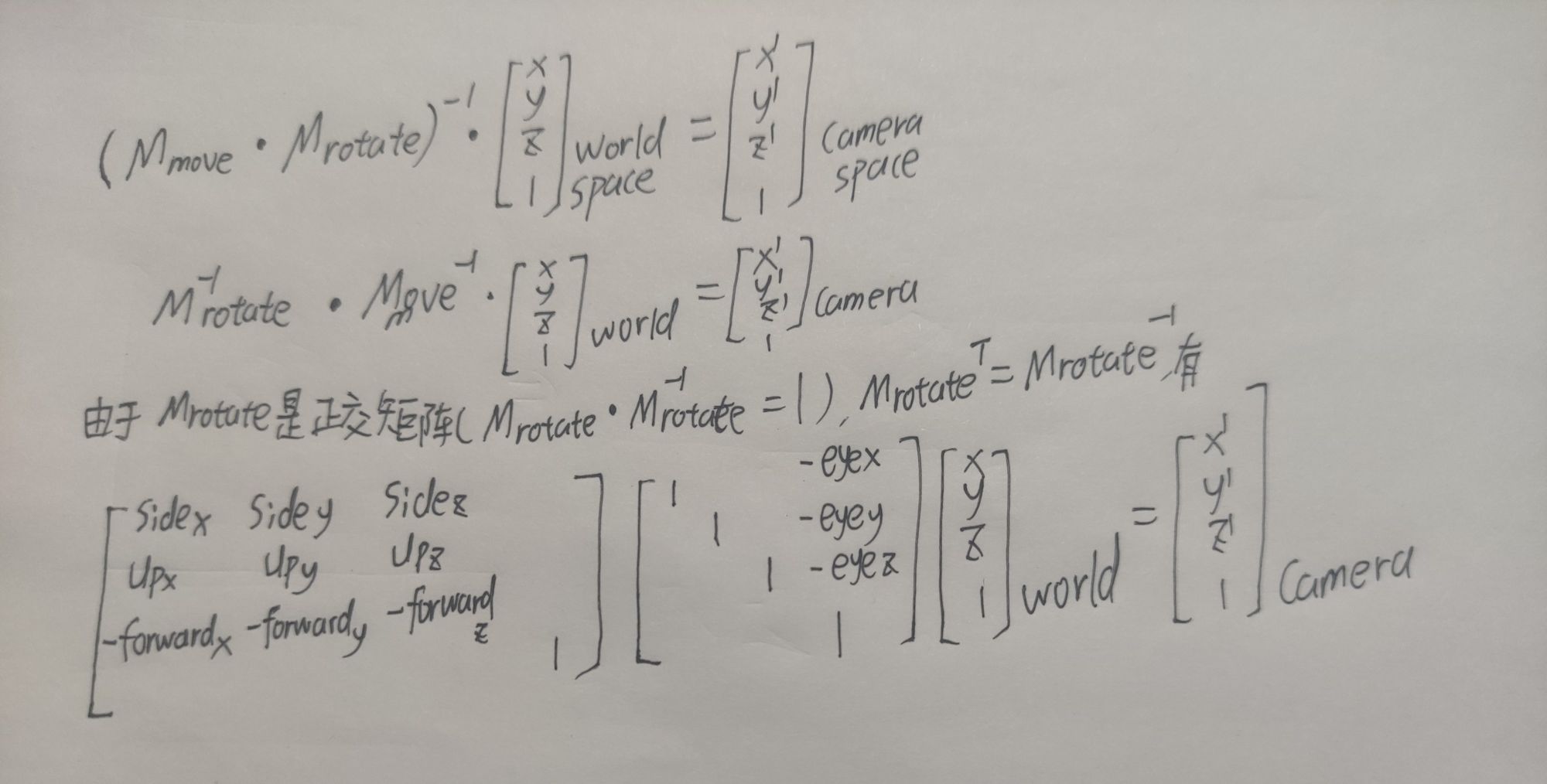
到这一步的所有坐标的z值都变成负数了,需要将其取反才能继续正确运算。
2.4 相机空间到投影空间矩阵
相机空间变换投影空间是将三维模型最终显示成二维视口的过程,模拟了照相机的调整焦距的过程。这部分我觉得是这几个变换里面最麻烦最难理解的(我前几次都是直接跳过了这部分的证明),但是多看几遍还是可以理解的!请不要放弃这里的证明。
透视投影详解这位博主写的非常好,我就是看他的这篇文章弄懂的,我这里是为了我的笔记完整,自己再写了一个自己理解的版本。
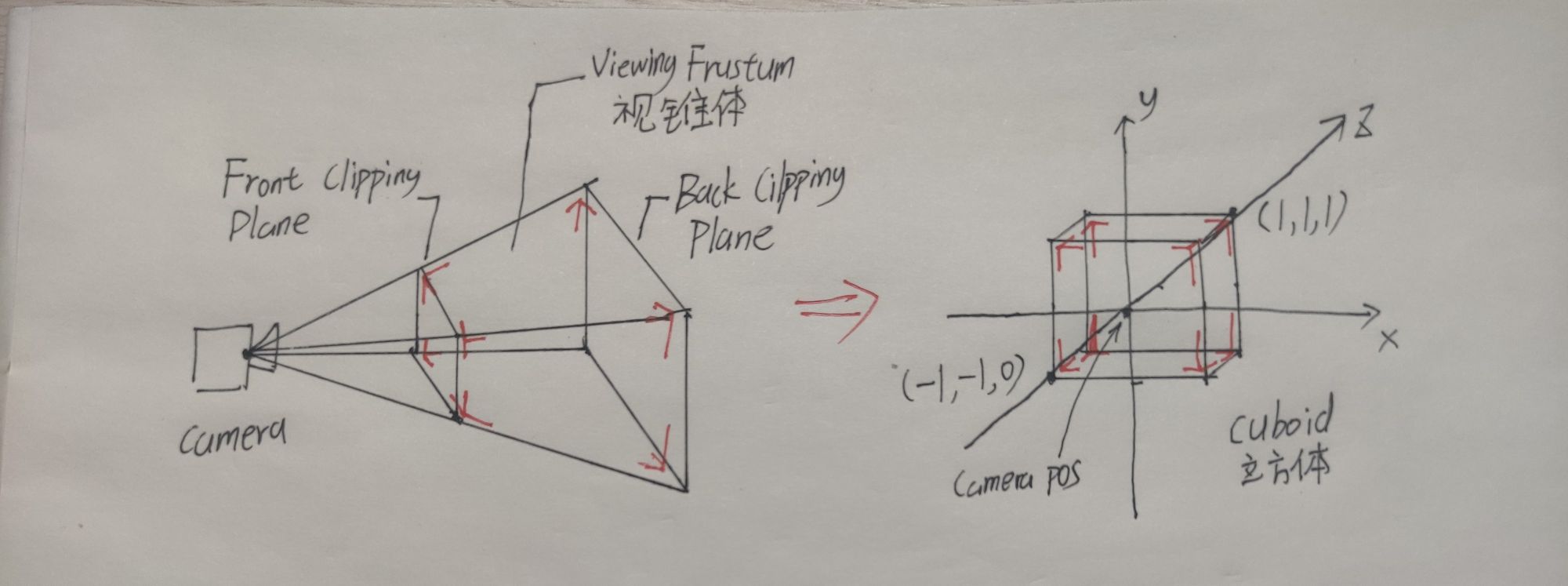
这个变换的全部就如上图所示,将摄像机拍摄到的一个棱锥区域转换成一个立方体区域。这个立方体将在最后的视口变换中最终变成二维图像。
棱锥区域叫做视锥体,是图左中红笔框起来的部分,由我们调整前后两个Clipping Plane确定,在该区域内的三维物体才会被最后捕获显示到最后的照片上。
立方体区域(cuboid),由视锥体转换而来,将棱锥前部分放大后部分缩小得到的,可以得到相机拍照的近大远小的效果,在靠近相机的物体在立方体内表现为靠近z=0的平面。变换最后的x坐标范围是[-1,1],y坐标范围是[-1,1],z坐标范围是[0,1]。
接下来就是这个变换矩阵的推导过程:
整个变换可以分成两部分:1.将视锥体里面的点投影到裁剪面上(这里我选择投影到前投影面(Front Clipping Plane),完全看个人,也可以投影到后投影面)2.将裁剪面上的点变换到立方体区域内
详细推导看下图:
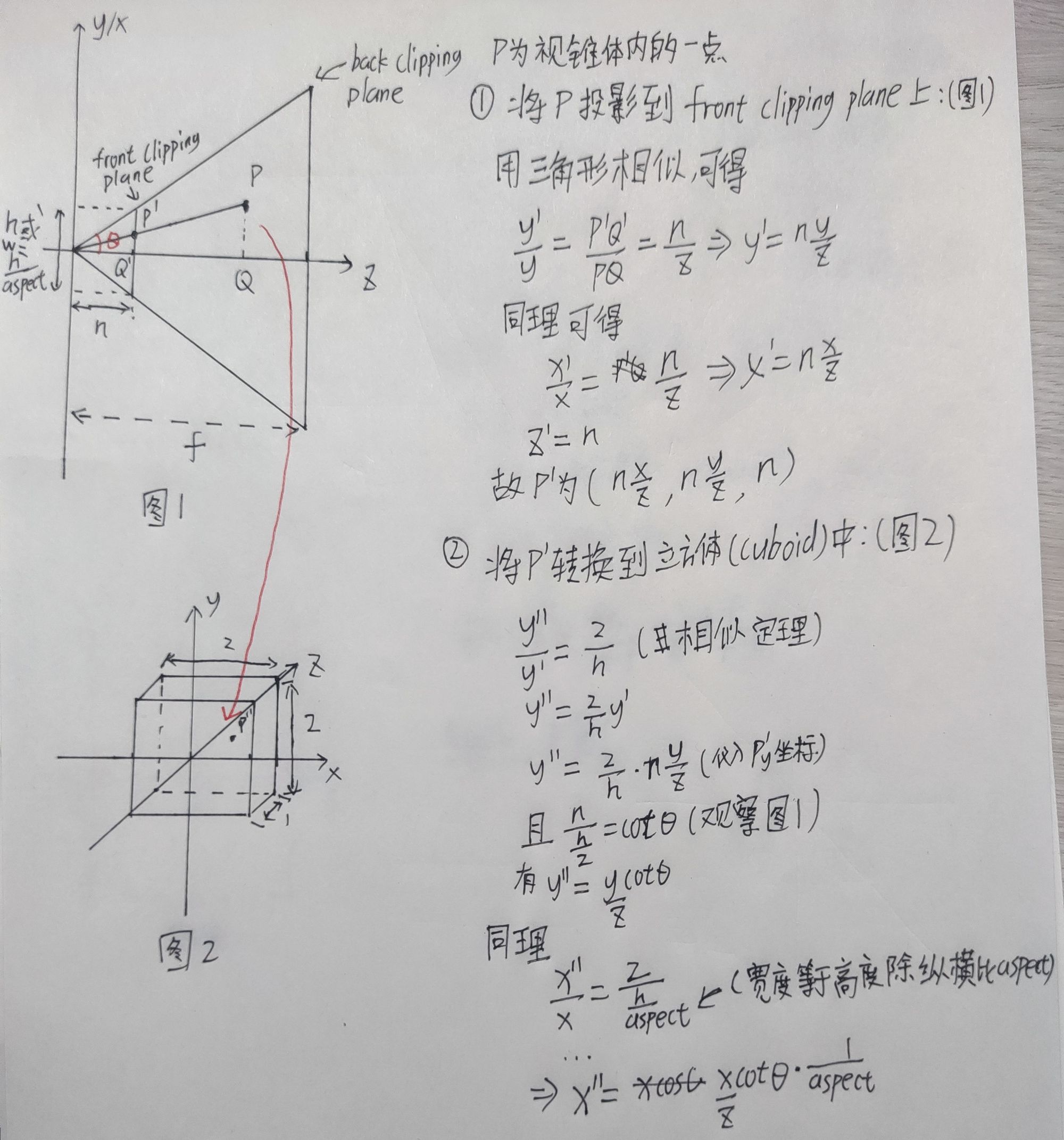
*aspect是横纵比w:h
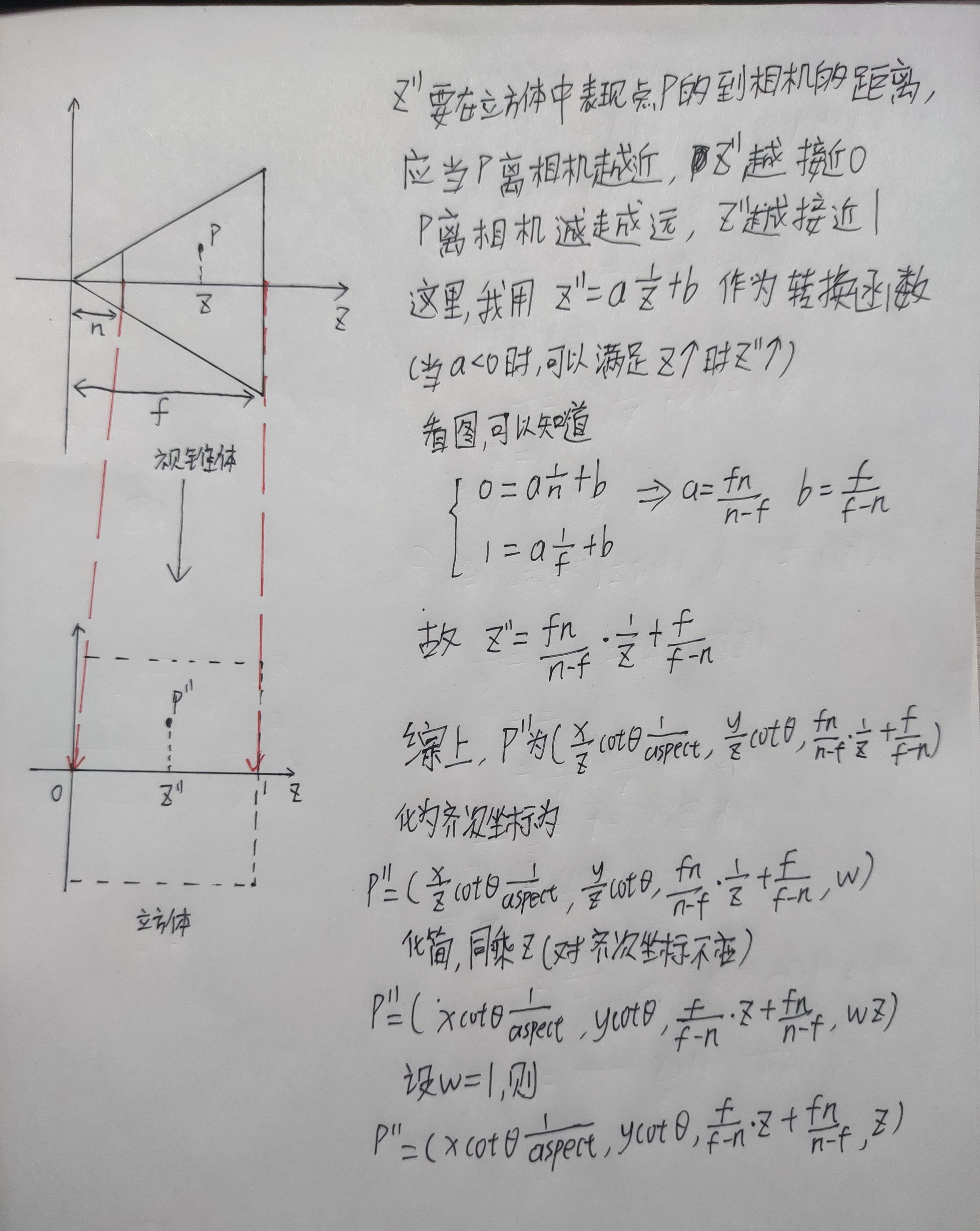
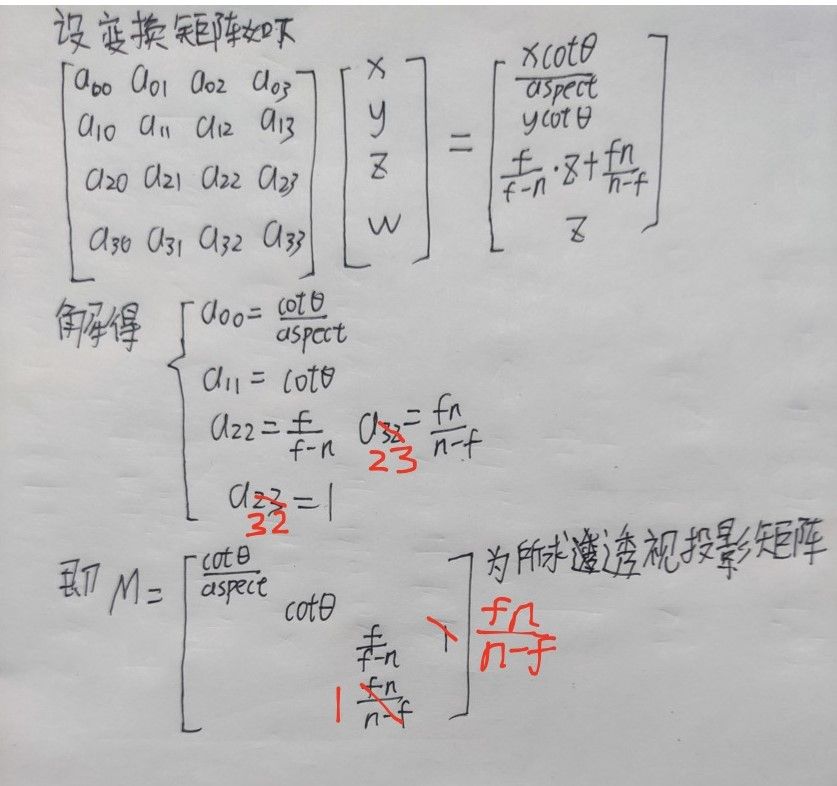
!需要注意w并不为1,需要将整个向量同除以w来把向量放在w=1的超平面上才能继续计算!
2.5 投影空间到屏幕空间矩阵
上个变换矩阵得到立方体(cuboid)之后,就差最后这一步就能够得到最后的相机拍摄的照片了,这一步也可以叫做视口变换,以下是详细的介绍:

2.6 总结
至此,全部的变换矩阵已经完成,通过这些变换就可以将三维模型转换成图像,接下来会写一个光栅化渲染器,用这些矩阵变换。
3. 参考链接
矩阵运算------四维齐次空间
图形学坐标变换1.物体到世界矩阵
Shader山下(十六)坐标空间与转换矩阵
透视投影详解
计算机图形学笔记-视图矩阵推导过程
DirectX视口变换矩阵详解
