1.简述

1.2什么是Bézier曲线

一种图形学中重要的参数曲线，由法国工程师皮埃尔·贝兹（Pierre Bézier）在1962年发表，所以叫做Bézier曲线。

教程： https://pomax.github.io/bezierinfo/zh-CN/index.html

1.2什么是B样条曲线

Bézier曲线的泛化，要表示一个复杂的曲线时,Bézier曲线需要特别多的控制点，控制点多起来开销就高，B样条的思想是通过把要表示的复杂曲线分段，每一段使用低阶的（比如二阶、三阶）Bézier曲线来表达，这样又可以表达复杂曲线，又可以节约性能与内存开销。

2.开源库 SISL 学习与探索

SISL是一个C++的全面的NURBS库，SISL代表着Sintef Spline Library，也就是由SINTEF数字数学与控制论学系的几何组开发的样条（spline）函数库。

https://github.com/SINTEF-Geometry/SISL

2.1构建

环境：Ubuntu 20.04 x64
构建方式参考SISL提供的manual手册：

$ cd <path_to_source_code>
$ mkdir build
$ cd build
$ cmake .. -DCMAKE_BUILD_TYPE=Release -Dsisl_COMPILE_VIEWER=ON    -Dsisl_COMPILE_EXAMPLES=ON

cmake上面的flag意思分别是生成Release版，编译查看器，编译样例

2.2 Examples

这个库提供了数十个example，展示了SISL库的具体应用与用法，由于我们只考虑二位的B样条曲线

2.2.1 example01

直接输入曲线的控制点生成一条曲线，曲线1，如下图

输入的点（图中小白点是输入的控制点）	生成的曲线1

2.2.2 example02

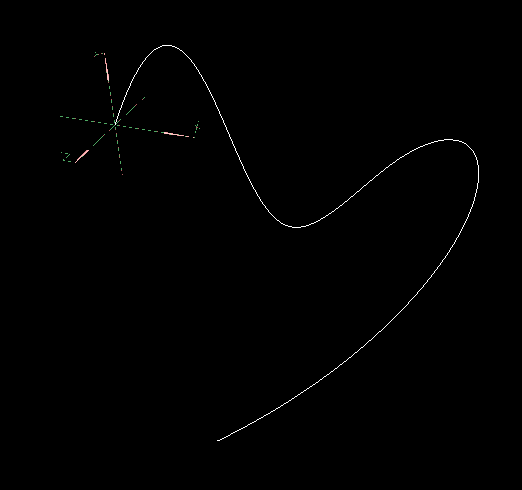
给定待拟合点集，interpolation 生成曲线，曲线2。

输入的待拟合点	根据拟合点生成的曲线2

2.2.3 example03

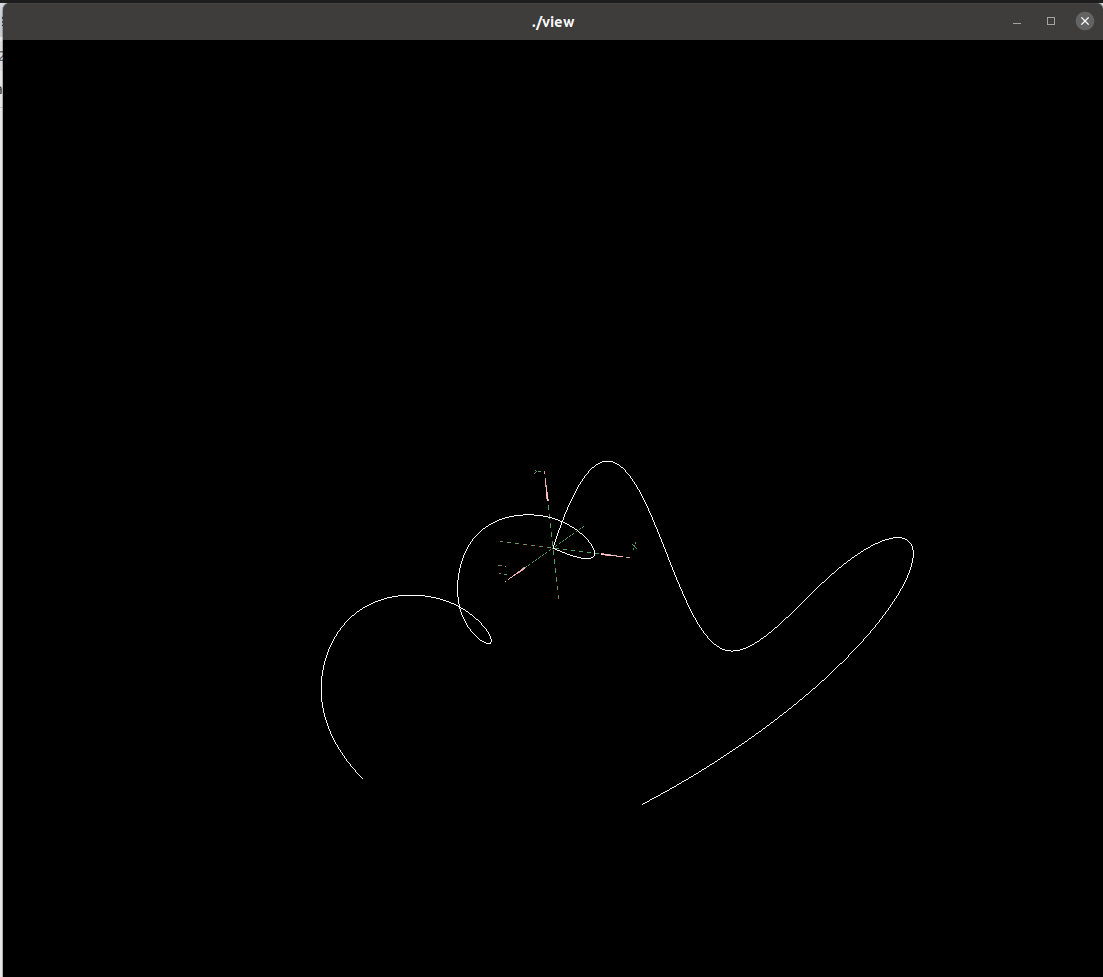
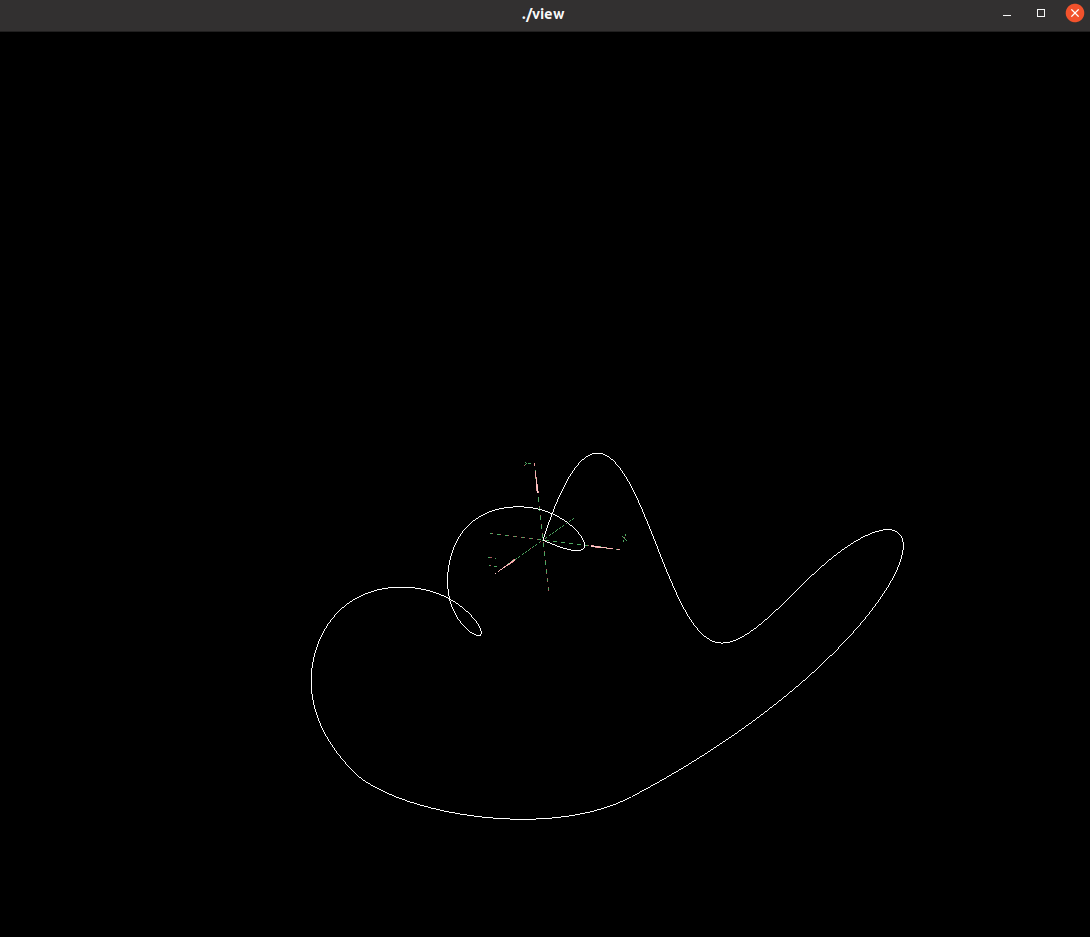
连接曲线1和曲线2,生成平滑的曲线3

曲线1和曲线2	加入曲线3后的平滑连接结果

2.2.4 example04

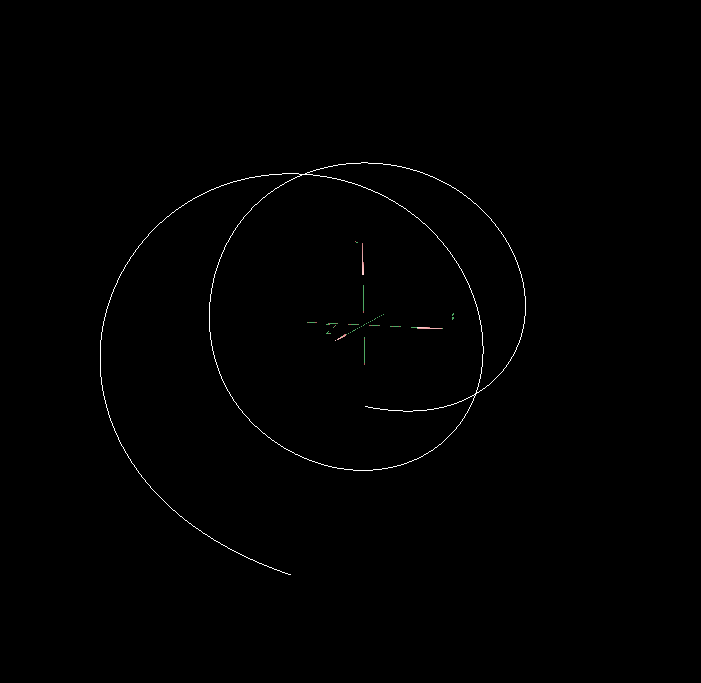
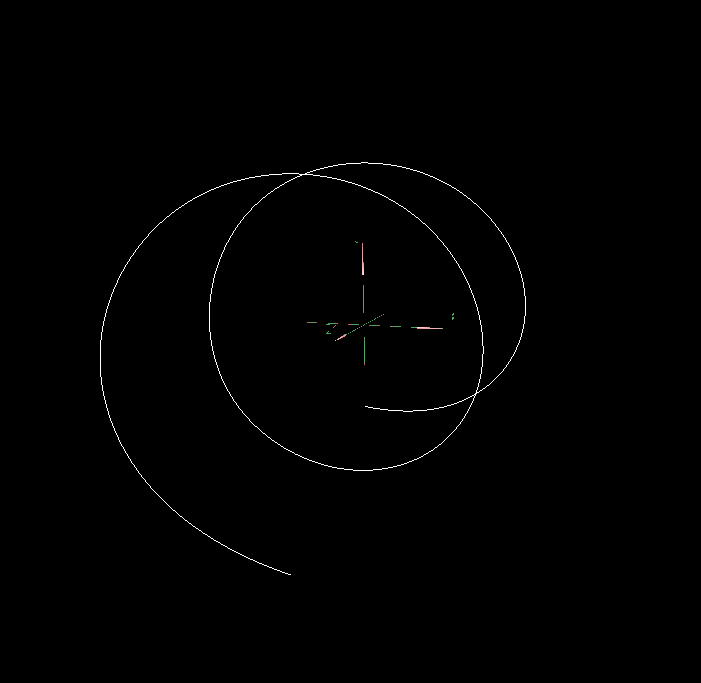
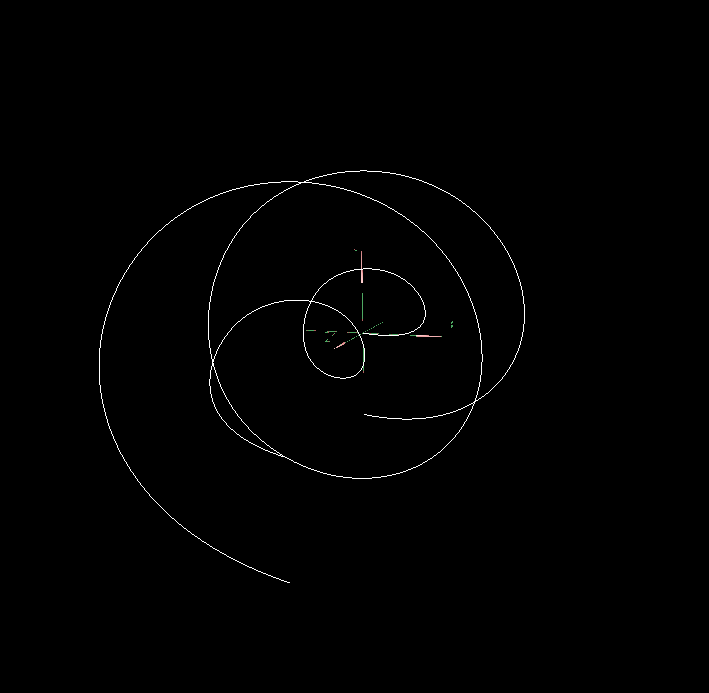
将曲线1添加offset，生成曲线4

原本的曲线1	添加offset后的曲线4	曲线1与添加offset后的曲线4

2.3 view

SISI库还带了一个简单的查看曲线曲面查看器，2.2节的截图都是出自这个查看器，下图是它的快捷键

First build viewer to see the result:
make sisl_view_demo
Then build

3.搭建拟合曲线演示环境

准备使用OpenCV + GLFW + GLAD + ImGui + OpenGL的调试环境来使用。
一个教程
https://blog.csdn.net/guduruyu/article/details/69220296